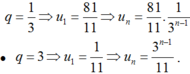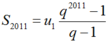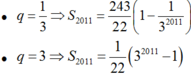Các câu hỏi tương tự
Cho dãy (un) thỏa mãn: \(\left\{{}\begin{matrix}u_1=5\\u_{n+1}=\dfrac{u^{2022}_n+3.u_n+16}{u_n^{2021}-u_n+11}\end{matrix}\right.\), ∀nϵN*
CMR (un) tăng
Cho dãy số u(n)=\(1/(2*4) +1/(5*7)+...+1/((3n-1)*(3n+1))\)
Tính Lim u(n).
Bài 1: Cho cấp số nhân có: u3 = 18 và u6 = -486.
Tìm số hạng đầu tiên và công bội q của cấp số nhân đó
Bài 2: Tìm u và q của cấp số nhân (un) biết:
Bài 3: Tìm cấp số nhân (un) biết cấp số đó có 4 số hạng có tổng bằng 360 và số hạng cuối gấp 9 lần số hạng thứ hai.
cho dãy số (un):\(\left\{{}\begin{matrix}u_1=\sqrt{3}+\sqrt{2}\\u_{n+1}=\left(\sqrt{3}-\sqrt{2}\right)u^2_n+\left(2\sqrt{6}-5\right)u_{n_{ }}+3\sqrt{3}-3\sqrt{2}\end{matrix}\right.\)
tìm lim(\(\Sigma^1_{i=1}\dfrac{1}{u_i+\sqrt{2}}\))
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số
u
(
n
)
xác định bởi
u
(
1
)
1
;
u
(
m
+
n
)
u...
Đọc tiếp
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Dãy số (��)(u
n) thỏa mãn ��≥�2u
≥n22 với mọi n. Tính lim un
.
Đọc tiếp
Dãy số thỏa mãn với mọi . Tính lim un
.
Câu 1: Có 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên ra 10 tấm thẻ. Xác suát để có 5 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn, trong đó chỉ có đúng 1 tấm thẻ mang số chia hết cho 5 là:
Câu 2:Từ các chữ số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 3?
Cho dãy số (U n) với U n = 2n/ n^2 + 1 , ∀ n ∈ N*
a) Viết 5 số hạng đầu
b) số 9/U¹ là hạng thứ mấy
c) chứng minh dãy số bị giảm và bị chặn