Phương pháp:
Công thức tổng quát của CSN có số hạng đầu là u 1
và công bội q : u n = u 1 . q n - 1
Cách giải:
Gọi q là công bội của CSN đã cho, ta có:
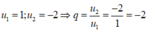
![]()
Chọn D
Phương pháp:
Công thức tổng quát của CSN có số hạng đầu là u 1
và công bội q : u n = u 1 . q n - 1
Cách giải:
Gọi q là công bội của CSN đã cho, ta có:
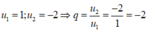
![]()
Chọn D
Trong mp Oxy, cho đường thẳng (d): 2018x + 2019y – 1 =0 và vectơ u → 2019 ; m . Tìm m để phép tịnh tiến theo vectơ u → biến (d) thành chính nó
A.–2018
B. –2019
C. 2018
D. 2019
1) cho cấp số nhân \(\left(u_n\right)\) có \(u_2=2\), \(u_6=32\) công bội của cấp số nhân đó là
2) cho cấp số nhân \(\left(u_n\right)\) có số hạng đầu \(u_1=2\) và công bội q = 3. Gía trị \(u_{2019}\) bằng
Bài 1: Cho cấp số nhân có: u3 = 18 và u6 = -486.
Tìm số hạng đầu tiên và công bội q của cấp số nhân đó
Bài 2: Tìm u và q của cấp số nhân (un) biết:
Bài 3: Tìm cấp số nhân (un) biết cấp số đó có 4 số hạng có tổng bằng 360 và số hạng cuối gấp 9 lần số hạng thứ hai.
Cho dãy số xác định bởi u1=1 , u n+1 = \(2un+\frac{n-1}{n^2+3n+2}\). khi đó u 2018 bằng
Có bao nhiêu giá trị nguyên của a thuộc khoảng (-2019; 2019) để l i m ( 4 n 2 + 3 n - 2 + a n - 3 ) = + ∞ ?
A. 2018
B. 2019
C. 2020
D. 2021
Tìm các giới hạn sau:
1/ \(\lim\limits_{x->-1}\) \(\dfrac{x^{2019}+1}{x^2+x}\)
2/ \(\lim\limits_{x->1}\) \(\dfrac{x+x^2+...+x^n-n}{x-1}\)
Cho u → = (3;-2), v → = (1;6) Khẳng định nào sau đây là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()