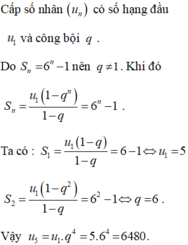Các câu hỏi tương tự
Cho cấp số nhân ( u n ) có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số cộng đã cho
A. 6480
B. 6840
C. 7775
D. 12005
Cho cấp số nhân
u
n
có tổng n số hạng đầu tiên là
S
n
5
n
−
1
,
n
1
,
2
,
3
...
Tìm số hạng đầu
u
1
và công bội q của cấp số nhân đó. A.
u
1
5...
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 5 n − 1 , n = 1 , 2 , 3 ... Tìm số hạng đầu u 1 và công bội q của cấp số nhân đó.
A. u 1 = 5 , q = 6
B. u 1 = 4 , q = 5
C. u 1 = 5 , q = 4
D. u 1 = 6 , q = 5
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là: A.
1
S
.
B.
1
q
n
.
S...
Đọc tiếp
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là:
A. 1 S .
B. 1 q n . S .
C. S q n − 1 .
D. q n S .
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Tổng n số hạng đầu tiên của một cấp số cộng
S
n
n
2
+
4
n
v
ớ
i
n
∈
N
*
. Tìm số hạng tổng quát
u
n
của cấp số cộng đã cho.
A
.
u
n
2
n
+
3...
Đọc tiếp
Tổng n số hạng đầu tiên của một cấp số cộng S n = n 2 + 4 n v ớ i n ∈ N * . Tìm số hạng tổng quát u n của cấp số cộng đã cho.
A . u n = 2 n + 3
B . u n = 3 n + 2
C . u n = 5 . 3 n - 1
D . u n = 5 . ( 8 5 ) n - 1
Cho cấp số nhân x n có tổng n số hạng đầu tiên là S n = 5 n - 1 . Giá trị của x 4 bằng
A. 2500
B. 624
C. 750
D. 500
Cho một cấp số nhân có các số hạng đều không âm thỏa mãn
u
2
6
,
u
4
24.
Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó. A.
3.2
12
−
3.
B.
2
12
−...
Đọc tiếp
Cho một cấp số nhân có các số hạng đều không âm thỏa mãn u 2 = 6 , u 4 = 24. Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.
A. 3.2 12 − 3.
B. 2 12 − 1.
C. 3.2 12 − 1.
D. 3.2 12 .
Cho một cấp số nhân có các số hạng đều không âm thỏa mãn
u
2
6
,
u
4
24
. Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó A.
3
.
2
12
-
3
B.
2
12
-
1
C.
3
....
Đọc tiếp
Cho một cấp số nhân có các số hạng đều không âm thỏa mãn u 2 = 6 , u 4 = 24 . Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó
A. 3 . 2 12 - 3
B. 2 12 - 1
C. 3 . 2 12 - 1
D. 3 . 2 12
Cho cấp số nhân
u
n
, biết
u
1
2
;
u
4
54
.
Tính
S
10
là tổng của 10 số hạng đầu tiên trong cấp số nhân đã cho? A.
S
10
118096
B.
S
10
59048...
Đọc tiếp
Cho cấp số nhân u n , biết u 1 = 2 ; u 4 = 54 . Tính S 10 là tổng của 10 số hạng đầu tiên trong cấp số nhân đã cho?
A. S 10 = 118096
B. S 10 = 59048
C. S 10 = - 59048
D. S 10 = 29524