Bạn xem lại đề nghen, đoạn thỏa mãn đó có vấn đề phải không nhỉ?
Bạn nên dùng Geogebra hoặc Desmos vẽ cái đường tròn kia sẽ dễ nhìn hơn, gửi nhầm vô phần cmt của bạn dưới nên mình gửi lại

Bạn xem lại đề nghen, đoạn thỏa mãn đó có vấn đề phải không nhỉ?
Bạn nên dùng Geogebra hoặc Desmos vẽ cái đường tròn kia sẽ dễ nhìn hơn, gửi nhầm vô phần cmt của bạn dưới nên mình gửi lại

Cho ba số thực x, y, z không âm thỏa mãn \(2^x+4^y+8^z=4\). Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S=\dfrac{x}{6}+\dfrac{y}{3}+\dfrac{z}{2}\). Đặt \(T=2M+6N\). Khẳng định nào dưới đây đúng?
A. \(T\in\left(1,2\right)\) B. \(T\in\left(2,3\right)\) C. \(T\in\left(3,4\right)\) D. \(T\in\left(4,5\right)\)
Giải chi tiết cho mình với ạ, mình cảm ơn nhiều ♥

Cho hai số thực dương x, y thỏa mãn \(2^x+2^y=4\). Tìm giá trị lớn nhất Pmax của biểu thức \(P=\left(2x^2+y\right)\left(2y^2+x\right)+9xy\)
Xét các số thực a, b thỏa mãn \(\left\{{}\begin{matrix}a\ge b^2\\b>1\end{matrix}\right.\). Tìm giá trị nhỏ nhất của \(P=\log_{\dfrac{a}{b}}a+\log_b\dfrac{b}{a}\)
1. Có bao nhiêu cặp số nguyên dương \(\left(m,n\right)\) sao cho \(m+n\le10\) và ứng với mỗi cặp \(\left(m,n\right)\) tồn tại đúng 3 số thực \(\alpha\in\left(-1;1\right)\) thỏa mãn \(2\alpha^m=nln\left(\alpha+\sqrt{\alpha^2+1}\right)\)
A. 7
B. 8
C. 10
D. 9
2. Xét các số thực \(x,y\) thỏa mãn \(2^{x^2+y^2+1}\le\left(x^2+y^2-2x+2\right)4^x\) GTNN của biểu thức \(P=\frac{8x+4}{2x-y+1}\) gần nhất với số nào dưới đây?
A. 1
B. 2
C. 3
D. 4
giải hệ
\(\left\{{}\begin{matrix}y\left[log_2\left(x-3\right)+log_3y\right]=x+1\\x^3-3x-y^3-6y^2-9y-2+ln\dfrac{x-1}{y+1}=0\end{matrix}\right.\)
Cho \(x\), \(y\), \(z\) \(\in\left[0;2\right]\) và thỏa mãn \(x+2y+z=6\). Tìm giá trị lớn nhất của biểu thức \(P=3^{2x-x^2}+5^{2y-y^2}+3^z+2x^2+4y^2\)
A. \(maxP=25\) B. \(maxP=26\)
C. \(maxP=27\) D. \(maxP=30\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥
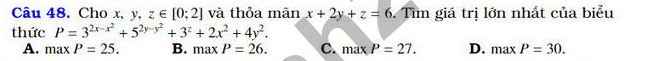
Cho số thực dương \(x,\left(x\ne1,x\ne\dfrac{1}{2}\right)\) thỏa mãn \(log_x\left(16x\right)=log_{2x}\left(8x\right)\). Giá trị \(log_x\left(16x\right)\) bằng \(log\dfrac{m}{n}\) với \(m\) và \(n\) là các số nguyên dương và phân số \(\dfrac{m}{n}\) tối giản. Tổng \(m+n\) bằng?
Giải thích cho mình dòng bôi vàng ở dưới, mình cảm ơn nhiều ♥

1. Cho hai số dương x, y thỏa mãn \(\log_2\frac{x^2+5y^2}{x^2+10xy+y^2}+1+x^2-10xy+9y^2\le0\). Gọi M, m lần lượt là GTLN, GTNN của \(P=\frac{x^2+xy+9y^2}{xy+y^2}\) Tính \(T=10M-m\)
A. 50
B. 60
C. 104
D. 94
2. Cho hai số dương x, y thỏa mãn \(\log_2\left(4x+y+2xy+2\right)^{y+2}=8-\left(2x-2\right)\left(y+2\right)\). GTNN của biểu thức \(P=2x+y\) có dạng \(M=a\sqrt{b}+c\) với a, b, c \(\in\) N, a>2. Tính \(S=a+b+c\)
A. 19
B. 3
C. 17
D. 7
47/004
Cho x,y là các số thực dương thỏa mãn \(log_{\frac{1}{3}}x+log_{\frac{1}{3}}y\le log_{\frac{1}{3}}\left(x+y^2\right)\). Tìm giá trị nhỏ nhất Pmin của biểu thức P = 2x + 3y