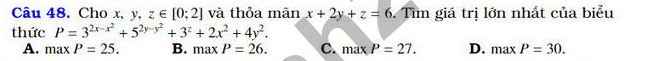Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)
\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)
Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)
\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)
\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)
\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)
(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))
Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này
Vậy giải cách khác:
\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)
Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)
\(\Rightarrow0\le2x-x^2\le1\)
Tương tự ta có: \(0\le2y-y^2\le1\)
Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)
\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)
\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)
\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)
\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)
Hoàn toàn tương tự, ta chứng minh được:
\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)
\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)
\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)
Lần này thì ko sai được rồi