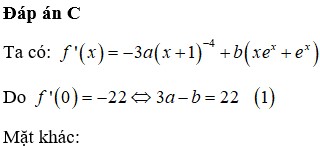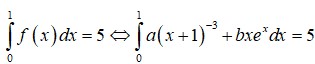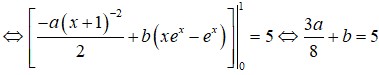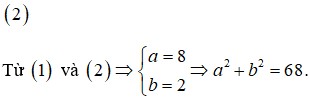Các câu hỏi tương tự
Cho các số thực a, b khác 0. Xét hàm số
f
(
x
)
a
(
x
+
1
)
3
+
b
x
e
x
với mọi x khác -1. Biết f(0)-22 và...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f ( x ) = a ( x + 1 ) 3 + b x e x với mọi x khác -1. Biết f'(0)=-22 và ∫ 0 1 f ( x ) d x = 5 . Tính a 2 + b 2 .
A. 42
B. 72
C. 68
D. 10
Cho các số thực a, b khác 0. Xét hàm số
f
x
a
x
+
1
3
+
b
x
e
x
với
∀
x
≠
−
1.
Biết
f
0
−
22
và
∫...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f x = a x + 1 3 + b x e x với ∀ x ≠ − 1. Biết f ' 0 = − 22 và ∫ 0 1 f x d x = 5. Tính a + b
A. 19
B. 7
C. 8
D. 10
Cho hàm số
f
(
x
)
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực và c
≠
0. Biết f(1)1, f(2)2 và f(f(x))x với mọi
x
≠
-
d
c
. Tính
l
i
m...
Đọc tiếp
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Cho các số thực a, b khác 0. Xét hàm số
f
x
a
x
+
1
3
+
b
x
e
x
với
∀
x
≠
−
1.
Biết
f
x
f
0
−
22...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f x = a x + 1 3 + b x e x với ∀ x ≠ − 1. Biết f ' x = f 0 = − 22 v à ∫ 0 1 f x d x = 5 . Tính a + b .
A. 19
B. 7
C. 8
D. 10
Cho hàm số
f
(
x
)
a
(
x
+
1
)
3
+
b
x
e
x
, biết f(0)-22 và
∫
0
1
f
(
x
)
d
x
5
. Tính Sa+b A. S10 B....
Đọc tiếp
Cho hàm số f ( x ) = a ( x + 1 ) 3 + b x e x , biết f'(0)=-22 và ∫ 0 1 f ( x ) d x = 5 .
Tính S=a+b
A. S=10
B. S=11
C. S=6
D. S=17
Cho hàm số đa thức bậc ba y f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0) A.
π
4
B. 0 C.
24
5
D. 2
Đọc tiếp
Cho hàm số đa thức bậc ba y = f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0)
A. π 4
B. 0
C. 24 5
D. 2
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số f (x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
,
f
(
1
)
ln
1
2
. Biết...
Đọc tiếp
Cho hàm số f (x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Biết ∫ 1 2 ( x 2 + 1 ) f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27 2
B. 1 6
C. 7 6
D. - 3 2
Cho hàm số f(x) liên tục trên R và f(x) ≠ 0 với mọi
x
∈
R
. f (x) (2x+1)f2(x) và f(1) –0,5. Biết rằng tổng f(1) + f(2) + f(3) + ... + f(2017)
a
b
; (a
∈
Z, b
∈
N) với
a
b
tối giản. Mệnh đề nào dưới đây đúng? A.
a
∈...
Đọc tiếp
Cho hàm số f(x) liên tục trên R và f(x) ≠ 0 với mọi x ∈ R . f '(x) = (2x+1)f2(x) và f(1) = –0,5. Biết rằng tổng f(1) + f(2) + f(3) + ... + f(2017) = a b ; (a ∈ Z, b ∈ N) với a b tối giản. Mệnh đề nào dưới đây đúng?
A. a ∈ - 2017 ; 2017
B. b - a = 4035
C. a + b = - 1
D. a b < - 1