Các câu hỏi tương tự
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Cho các số thực a. Giá trị của biểu thức
A
log
2
1
2
a
+
log
2
1
2
b
bằng giá trị của biểu thức nào trong các biểu thức sau đây? A. −a−b B. −ab C. a +b D. ab
Đọc tiếp
Cho các số thực a. Giá trị của biểu thức A = log 2 1 2 a + log 2 1 2 b bằng giá trị của biểu thức nào trong các biểu thức sau đây?
A. −a−b
B. −ab
C. a +b
D. ab
Cho
∫
0
1
1
(
x
+
3
)
(
x
+
1
)
3
d
x
a
-
b
với a,b là các số n...
Đọc tiếp
Cho ∫ 0 1 1 ( x + 3 ) ( x + 1 ) 3 d x = a - b với a,b là các số nguyên. Giá trị của biểu thức a b + b a bằng
A. 17.
B. 57.
C. 145.
D. 32.
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức gần với giá trị nào nhất trong các đáp án sau: A. 4,65 B. 4,66 C. 4,67 D. 4,64
Đọc tiếp
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 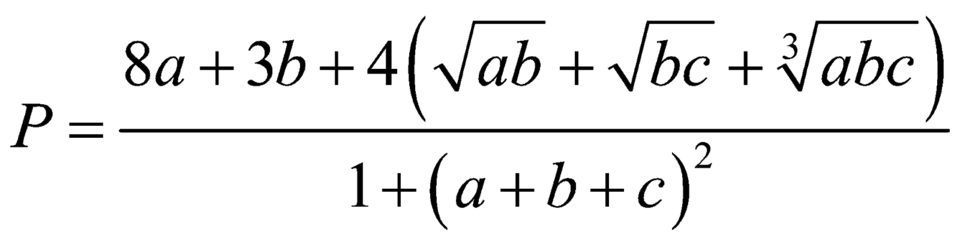 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
Cho a,b,c là các số thực dương khi đó giá trị lớn nhất của biểu thức 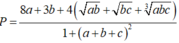 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
A. 4,65
B. 4,66
C. 4,67
D. 4,64
cho ba số thực dương a b c thỏa mãn ab+bc+ac≤1. tìm giá trị nhỏ nhất của biểu thức P biết:
P= \(\dfrac{1}{\sqrt{a^2+b^2-abc}}+\dfrac{1}{\sqrt{a^2+c^2-abc}}+\dfrac{1}{\sqrt{c^2+b^2-abc}}\)
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Tính giá trị bằng số của biểu thức log a 2 a (a > 0; a ≠ 1)
A. 2 B. -2
C. 1/2 D. -1/2







