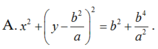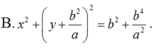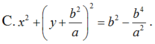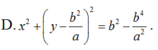(C): \(\left(x-a\right)^2+\left(y-b\right)^2=25\)
=>Tâm là I(a;b); R=5
I(a;b); A(1;-1)
\(\overrightarrow{IA}=\left(1-a;-1-b\right)\)
(d): 3x+4y+1=0
=>Vecto pháp tuyến là (3;4)
=>Vecto chỉ phương là (-4;3)
Vì (d) tiếp xúc với (C) nên \(\left(1-a\right)\cdot\left(-4\right)+3\left(-1-b\right)=0\)
=>4(a-1)-3(b+1)=0
=>4a-4-3b-3=0
=>4a-3b-7=0
=>3b=4a-7
=>\(b=\dfrac{4}{3}a-\dfrac{7}{3}\)
\(IA^2=25\)
=>\(\left(a-1\right)^2+\left(b+1\right)^2=25\)
=>\(\left(a-1\right)^2+\left(\dfrac{4}{3}a-\dfrac{7}{3}+1\right)^2=25\)
=>\(\left(a-1\right)^2+\left(\dfrac{4}{3}a-\dfrac{4}{3}\right)^2=25\)
=>\(\dfrac{25}{9}\left(a-1\right)^2=25\)
=>\(\left(a-1\right)^2=9\)
=>\(\left[{}\begin{matrix}a-1=3\\a-1=-3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}a=4\\a=-2\end{matrix}\right.\)
Khi a=4 thì \(b=\dfrac{4}{3}\cdot4-\dfrac{7}{3}=\dfrac{16}{3}-\dfrac{7}{3}=\dfrac{9}{3}=3\)
Khi a=-2 thì \(b=\dfrac{4}{3}\cdot\left(-2\right)-\dfrac{7}{3}=-\dfrac{8}{3}-\dfrac{7}{3}=-5\)