Chọn đáp án C.
Điều kiện x ≥ 0 ; x ≠ 1 ; x ≠ 4 .
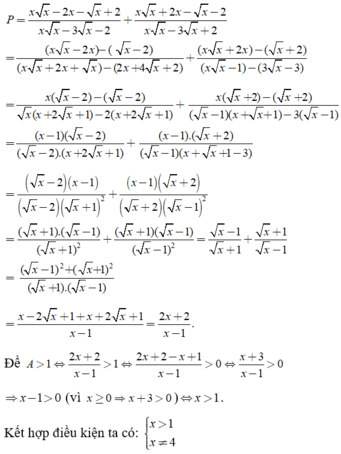
Chọn đáp án C.
Điều kiện x ≥ 0 ; x ≠ 1 ; x ≠ 4 .
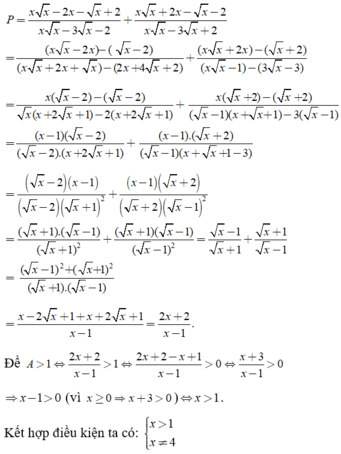
Cho biểu thức
A=2/√x -1 +2(√x +1)/x+√x +1 +x-10√x +3/√x^3 -1
1. Với giá trị nào của x thì biểu thức có nghĩa
2. Rút gọn biểu thức
cho biểu thức: A=\(\dfrac{x^2+x-2}{x},B=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{x^2-1}\)
a)tính giá trị biểu thức với A=3
b)rút gọn biểu thức B
c)tìm giá trị của x để biểu thức P=A.B đạt giá trị nhỏ nhất
Với giá trị nào của x thì các biểu thức sau có nghĩa?
a,Căn 2(x + 3)
b,Căn x^2 - x + 1
c,Căn x -1 / căn x + 1 (dấu căn của mình x)
Bài 3: Cho biểu thức A =\(\dfrac{x+1-2\sqrt{x}}{\sqrt{x}-1}+\dfrac{x+\sqrt{x}}{\sqrt{x}+1}\)
a)Đặt điều kiện để biểu thức A có nghĩa; b)Rút gọn biểu thức A;
c)Với giá trị nào của x thì A< - 1
Cho biểu thức
\(A=\left(\frac{x-3\sqrt{x}}{x-9}\right):\left(\frac{1}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
1. Rút gọn biểu thức A
2. Tính giá trị của A tại \(x=\frac{25}{16}\)
3. Với giá trị nào của x thì biểu thức A nhận giá trị âm
4. Tính giá trị của A sau khi \(x=\sqrt{7-2\sqrt{6}}+3\)
3. cho biểu thức A = \(\sqrt{x^2+2\sqrt{x^2-1}}-\sqrt{x^2-2x\sqrt{x^2-1}}\)
a. với giá trị nào của x thì A có nghĩa
b. tíng A nếu x ≥\(\sqrt{2}\)
a) Với giá trị nào của x thì các biểu thức sau đây xác định :
\(\sqrt{3x+4}\) \(\sqrt{\dfrac{-1}{2x+2}}\)
b) Rút gọn biểu thức B = \(\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\) với x ≥ 0 , x ≠ 1
c) Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
D = \(\dfrac{2\sqrt{x-1}}{\sqrt{x}+3}\)
cho biểu thức A= \(\left(\frac{x-3\sqrt{x}}{x-9}-1\right):\left(\frac{9-x}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}+3}\right)\)
( Với x lớn hơn hoặc bằng 0; x khác 2 và 9)
a) Rút gọn biểu thức A
b) Với giá trị nào của x thì A có giá trị = 1/2
c) tính giá trị cuả A tại x= \(19-8\sqrt{3}\)
d) tính số nguyên X để biểu thức A có giá trị là số nguyên ?
Bài 4: Cho biểu thức : B = \(\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
a) Tìm TXĐ rồi rút gọn biểu thức B; b) Tính giá trị của B với x =3;
c) Tìm giá trị của x để |A|=\(\dfrac{1}{2}\).
Cho biểu thức A=2√x - 3/√x - 2 và B=2/√x+3 + √x/√x-3 + 4√x/9-x với x≥0; x≠4; x≠9. a) tính giá trị biểu thức A khi x thỏa mãn |x-2|=2. b) rút gọn biểu thức B. c) đặt C=A.B. Tìm x để C≥1.