Các câu hỏi tương tự
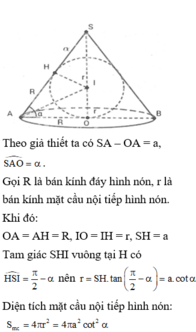
Cho biết hiệu đường sinh và bán kính đáy của một hình nón là a, góc giữa đường sinh và mặt đáy là α. Tính diện tích mặt cầu nội tiếp hình nón A.
S
m
c
3
π
a
2
c
o
t
2
α
B.
S
m
c...
Đọc tiếp
Cho biết hiệu đường sinh và bán kính đáy của một hình nón là a, góc giữa đường sinh và mặt đáy là α. Tính diện tích mặt cầu nội tiếp hình nón
A. S m c = 3 π a 2 c o t 2 α
B. S m c = 4 π a 2 c o t 2 α
C. S m c = 2 π a 2 c o t 2 α
D. S m c = π a 2 c o t 2 α
Trong không gian Oxyz cho mặt cầu (S):
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
3
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 27 . Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0;-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng ( α ) có phương trình dạng ax+by-z+c= 0, khi đó a-b+c bằng:
A. -4.
B. 8
C. 0
D. 2
Cho hình nón có đường sinh là a, góc giữa đường sinh và đáy là
α
. Tính diện tích xung quanh của hình nón. A.
2
πa
2
sinα
B.
πa
2
sinα
C.
2
πa
2
cos
α
D.
πa
2
cos
α
Đọc tiếp
Cho hình nón có đường sinh là a, góc giữa đường sinh và đáy là α . Tính diện tích xung quanh của hình nón.
A. 2 πa 2 sinα
B. πa 2 sinα
C. 2 πa 2 cos α
D. πa 2 cos α
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R3cm, góc ở đỉnh hình nón là
α
120
°
. Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng A.
3
3
c
m
2
B.
6
3
c
m...
Đọc tiếp
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh hình nón là α = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất. A.
4
r
3
B.
r
3
C.
r
6
D.
7
r
6
Đọc tiếp
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất.
A. 4 r 3
B. r 3
C. r 6
D. 7 r 6
Trong không gian Oxyz cho mặt cầu
S
:
x
−
1
2
+
y
+
2
2
+
z
−
3
2
27
. Gọi
α
là mặt phẳn...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu S : x − 1 2 + y + 2 2 + z − 3 2 = 27 . Gọi α là mặt phẳng đi qua hai điểm A 0 ; 0 ; − 4 , B 2 ; 0 ; 0 và cắt S theo giao tuyến là đường tròn (C) sao cho khối nón có đỉnh là tâm của (S), đáy là (C) có thể tích lớn nhất. Biết mặt phẳng α có phương trình dạng a x + b y − z + c = 0 , khi đó a − b + c bằng:
A. - 4
B. 8
C. 0
D. 2
Một hình nón có chiều cao
S
O
50
c
m
và có bán kính đáy bằng
10
c
m
.
Lấy điểm M thuộc đoạn SO sao cho
O
M
20
c
m
.
Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn
C
. Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi
C...
Đọc tiếp
Một hình nón có chiều cao S O = 50 c m và có bán kính đáy bằng 10 c m . Lấy điểm M thuộc đoạn SO sao cho O M = 20 c m . Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn C . Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi C (xem hình vẽ).
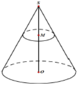
A. 16 π 26 c m 2
B. 26 π 26 c m 2
C. 36 π 26 c m 2
D. 46 π 26 c m 2
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
4
x
+
6
y
-
3
0
và điểm A(2;1;-2). Đườn...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 4 x + 6 y - 3 = 0 và điểm A(2;1;-2). Đường thẳng d đi qua A, tiếp xúc với (S) tại M luôn nằm trên mặt nón (N) cố định. Tọa độ tâm đường tròn đáy của (N) là H(a;b;c). Giá trị 3a-2b+c bằng
A. 8.
B. 4
C. 2.
D. 6 5
Trong không gian Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
+
2
2
+
z
-
3
2
48
. Gọi
α
là mặt phẳ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x - 1 2 + y + 2 2 + z - 3 2 = 48 . Gọi α là mặt phẳng đi qua hai điểm A(0;0-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C). Khối nón (N) có đỉnh là tâm của (S), đường tròn đáy là (C) cỏ thể tích lớn nhất bằng
A. 128 π 3
B. 39 π
C. 88 π 3
D. 215 π 3