Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Độ dài cạnh của tam giác đều nội tiếp đường tròn (O;R) bằng
A. R/2; B. (R 3 )/2;
C. R 3 D. Một đáp án khác.
Hãy chọn phương án đúng.
Cho h.bs.23, trong đó OA = 3, O’A = 2, AB = 5. Độ dài AC bằng
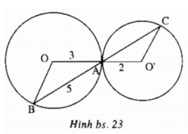
A. 10/3; B. 3,5;
C. 3; D. 4.
Hãy chọn phương án đúng.
Tỉ số bán kính đường tròn nội tiếp và đường tròn ngoại tiếp một tam giác đều bằng
A. 1/3; B. 1/2;
C. 1/ 2 ; D. 2.
Hãy chọn phương án đúng.
(1) rút gọn biểu thức:
a) A= \(3\sqrt{2}+5\sqrt{8}-2\sqrt{50}\)
b) B= \(\sqrt{7-4\sqrt{3}}+\sqrt{12+6\sqrt{3}}\)
c) C= \(\dfrac{1}{3+\sqrt{5}}+\dfrac{1}{3-\sqrt{5}}\)
d) D= \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\)
giúp mk vs ạ mai mk hc rồi
1. Cho A {a,b,c}, B{b,c,d}, C{b,c,e}, lựa chọn phương án đúng:A. (A∪B)∩C(A∪B)∩(A∪C)(A∪B)∩C(A∪B)∩(A∪C)B. (A∩B)∪C(A∪B)∩C(A∩B)∪C(A∪B)∩CC. A∪(B∪C)(A∪B)∩CA∪(B∪C)(A∪B)∩CD. A∪(B∩C)(A∪B)∩CA∪(B∩C)(A∪B)∩CA đúng hay D đúng??? 2. A và B là 2 tập hợp có hữu hạn phần tử và A∩BBA∩BB B có là tập con thực sự của A hay ko, tại sao???3. Cho A là tập các số nguyên dương chia hết cho 3B là tập hợp các số nguyên dương chia hết cho 7C là tập hợp các số nguyên dương chia hết cho 6D là tập hợp các số nguyên dương chia...
Đọc tiếp
1. Cho A ={a,b,c}, B={b,c,d}, C={b,c,e}, lựa chọn phương án đúng:
A. (A∪B)∩C=(A∪B)∩(A∪C)(A∪B)∩C=(A∪B)∩(A∪C)
B. (A∩B)∪C=(A∪B)∩C(A∩B)∪C=(A∪B)∩C
C. A∪(B∪C)=(A∪B)∩CA∪(B∪C)=(A∪B)∩C
D. A∪(B∩C)=(A∪B)∩CA∪(B∩C)=(A∪B)∩C
A đúng hay D đúng???
2. A và B là 2 tập hợp có hữu hạn phần tử và A∩B=BA∩B=B >> B có là tập con thực sự của A hay ko, tại sao???
3. Cho A là tập các số nguyên dương chia hết cho 3
B là tập hợp các số nguyên dương chia hết cho 7
C là tập hợp các số nguyên dương chia hết cho 6
D là tập hợp các số nguyên dương chia hết cho 21
E là tập hợp các số nguyên dương chia hết cho 18
Lựa chọn phương án đúng.
A. A∪C=EA∪C=E
B. A⊂CA⊂C
C. A∩C=EA∩C=E
D. A∩B=DA∩B=D
B sai ở đâu???
Bài 1: Cho a,b,c∈Z,\(a^2+b^2+c^2⋮9\). CMR: abc⋮3
Bài 2: Cho a,b,c,d bất kì nguyên. CMR:\(\left(a-b\right)\left(a-c\right)\left(a-d\right)\left(b-c\right)\left(b-d\right)\left(c-d\right)⋮12\)
Bài 3: Tìm \(n\in N\)*:\(n.2^n+3^n⋮5\)
Rút gọn các biểu thức sau a)√27-✓12+✓48-5✓3 b)5✓18-✓5+✓20+✓1 2 C)✓25:✓16=✓36:✓9 D)✓12+✓27-5✓3 E)2✓3-✓75+2✓12
Cho 3 số dương a,b,c thỏa mãn \(a^2+b^2+c^2=27\). Chứng minh: \(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\ge\frac{12}{a^2+63}+\frac{12}{b^2+63}+\frac{12}{c^2+63}\)
cho a,b,c,d >0 và 2(a+b+c+d)>-abcd chứng minh a^2+b^2+c^2+d^2>=abcd
bài 2 cho a,b,c>0 và a+b+c>=abc chứng minh có ít nhất 2 trong 3 bdt sau là đúng 2/a +3/b+ 6/c>=6 2/b + 3/c+ 6/a>=6 2/c + 3/a +6/b >=6