7 tháng 10 lúc 18:48
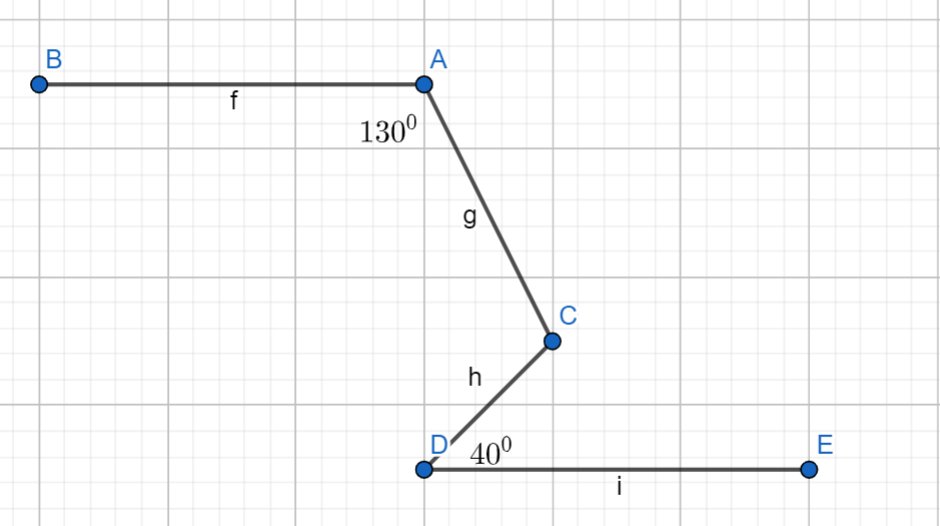
Qua C, kẻ tia CF nằm giữa hai tia CD và CA sao cho CF//AB//DE
CF//AB
=>\(\widehat{BAC}+\widehat{ACF}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{ACF}=180^0-130^0=50^0\)
Ta có: CF//DE
=>\(\widehat{FCD}=\widehat{CDE}\)(hai góc so le trong)
=>\(\widehat{FCD}=40^0\)
\(\widehat{ACD}=\widehat{ACF}+\widehat{FCD}=50^0+40^0=90^0\)
Đúng 2
Bình luận (0)
