Question

Cho ▲ABC vuông tại C (AC< BC) đường cao CK và phân giác BD qua D kẻ đường thẳng vuông góc với AC cắt CK tại H, cắt AB tại I. Chứng minh ▲DCH đồng dạng ▲CBA và AD.AC=DH.AB 

Answer 1

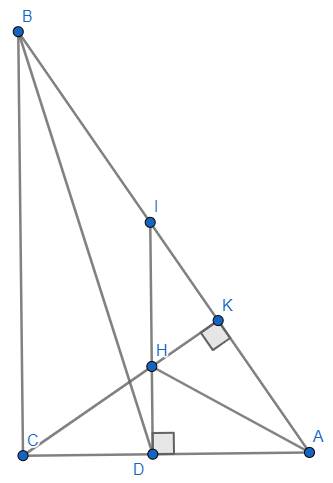
Xét \(\Delta DCH,\Delta CBA\) có : \(\left\{{}\begin{matrix}\hat{CDH}=\hat{ACB}=90^o\left(gt\right)\\\hat{DCH}=\hat{CBA}\left(\text{cùng phụ với góc A}\right)\end{matrix}\right.\)

\(\Rightarrow\Delta DCH\sim\Delta CBA\left(g.g\right)\) (đpcm).

\(\Rightarrow\dfrac{DH}{AC}=\dfrac{CD}{BC}\)

Ta cũng có : \(BD\) là phân giác nên : \(\dfrac{AD}{CD}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}\)

Suy ra : \(\dfrac{DH}{AC}=\dfrac{AD}{AB}\Rightarrow AD.AC=DH.AB\) (đpcm).