+ M S E ^ là góc có đỉnh S ở trong đường tròn (O)
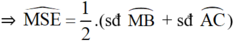
+ E S M ^ là góc tạo bởi tiếp tuyến ME và đây MC
⇒ E M S ^ = 1 2 . s đ M C ⏜ = 1 2 . s đ M B ⏜ + s đ B C ⏜


+ M S E ^ là góc có đỉnh S ở trong đường tròn (O)
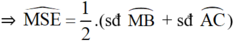
+ E S M ^ là góc tạo bởi tiếp tuyến ME và đây MC
⇒ E M S ^ = 1 2 . s đ M C ⏜ = 1 2 . s đ M B ⏜ + s đ B C ⏜

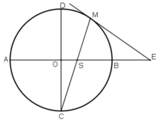
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.
Bài tập: Cho AB và CD là 2 đkinh vuông góc của đtron (o). Trên cung nhỏ BD lấy điểm M. Tiếp tuyến M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES=EM
cho (O) và 2 đường kính AB và CD vuông góc với nhau. Trên cung BD lấy 1 điểm M. Tiếp tuyến của (O) tại M cắt AB ở E; CM cắt AB tại F . Chứng minh EF = EM
cho (O) và 2 đường kính AB và CD vuông góc với nhau. Trên cung BD lấy 1 điểm M. Tiếp tuyến của (O) tại M cắt AB ở E; CM cắt AB tại F . Chứng minh EF = EM
Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
Cho đường tròn tâm O có hai đường kính là AB và CD vuông góc với nhau tại O. Trên cung nhỏ BC lấy điểm M, AM cắt CD tại I. Tiếp tuyến của O tại M cắt tia AB tại N. Chứng minh rằng: AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CMI.
Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
d, Cho EM = R, tính FA.SM theo R
e, Kẻ MH ⊥ AB. Xác định vị trí điểm M để tam giác MHO có diện tích đạt giá trị lớn nhất
Bài 4: (3,5 điểm) Cho đường tròn (O ; R) đường kính AB và điểm M bất kì thuộc đường tròn (M ≠ A, B) . Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt AN ở D.
a) Chứng minh: 4 điểm A, D, M , O cùng thuộc một đường tròn
b) Chứng minh: OD // BM và suy ra D là trung điểm của AN
c) Đường thẳng kẻ qua O và vuông góc với BM cắt tia DM ở E. Chứng minh: BE là tiếp tuyến của đường tròn (O ; R)
d) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm của AI và BD là J. Khi điểm M di động trên (O ; R) thì J chạy trên đường nào?
Cho đường tròn (O;R) đường kính AB. Kẻ đường kính CD vuông góc với AB. Lấy điểm M thuộc cung nhỏ BC,AM cắt CD tại E. Qua kẻ tiếp tuyến với đường tròn (O) cắt đường thẳng BM tại N . Chứng minh bốn điểm M,N,D,E cùng nằm trên một đường tròn