Ta có ![]()
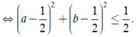
Ta có 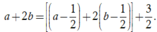
Áp dụng bất đẳng thức Bunhiacopxky, ta có
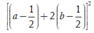
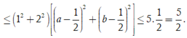
Do đó 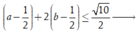
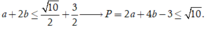
Dấu "x" xảy ra 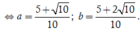
Chọn C.
Ta thấy (1) là hình tròn tâm ![]()
Ta có ![]() Xem đây là phương trình đường thẳng.
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung ![]()

Ta có ![]()
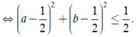
Ta có 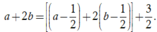
Áp dụng bất đẳng thức Bunhiacopxky, ta có
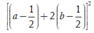
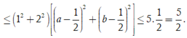
Do đó 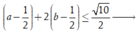
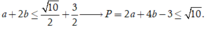
Dấu "x" xảy ra 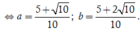
Chọn C.
Ta thấy (1) là hình tròn tâm ![]()
Ta có ![]() Xem đây là phương trình đường thẳng.
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung ![]()

Cho hai số thực a,b thỏa mãn điều kiện a 2 + b 2 > 1 và log a 2 + b 2 a + b ≥ 1 . Giá trị lớn nhất của biểu thức P = 2a + 4b – 3 là
A. 2 10
B. 10
C. 10 2
D. 1 10
Cho các số thực a, b, c thỏa mãn a 2 + b 2 + c 2 - 2 a - 4 b = 4 . Tính P = a + 2b + 3c khi biểu thức đạt giá trị lớn nhất
A. 7.
B. 3
C. -3.
D. -7.
Cho hai số thực dương a, b thỏa mãn 9 a 3 + a b + 1 = 3 b + 2 . Giá trị lớn nhất của biểu thức S = 6a - b là
A. 17 12
B. 82 3
C. 11 3
D. 89 12
Cho các số thực a và b thỏa mãn: ( 2 + a ) ( 1 + b ) = 9 2 Giá trị nhỏ nhất của biểu thức: P = 16 + a 4 + 4 1 + b 4 nằm trong khoảng
A. (8,1;8,3)
B. (4;4,2)
C. (8,3;8,5)
D. (12,4;12,6)
Cho số phức z=a+bi ( a , b ∈ R ) thỏa mãn |z-1-2i|= 3 . Khi biểu thức P = | z + 3 | 2 - | z - 2 i | 2 đạt giá trị lớn nhất. Giá trị của [ a b ] bằng
A. 14.
B. 13.
C. 7.
D. 8.
Cho hai số thực a,b thỏa mãn a > 0,0 < b < 2 . Tìm giá trị nhỏ nhất của biểu thức P = ( 2 b ) a 2 a − b a 2 + 2 a + 2 b a 2 b a
A. P min = 9 4 .
B. P min = 7 4 .
C. P min = 13 4 .
D. P min = 4.
Cho các số thực a, b thỏa mãn 0 < a < 1 < b ; a b > 1 . Giá trị lớn nhất của biểu thức P = log a a b + 4 1 - log a b log a b a b bằng
A. 3.
B. -4
C. 4.
D. 2
Cho a,b là các số thực dương thỏa mãn b>1 và a ≤ b < a . Giá trị nhỏ nhất của biểu thức P = log a b a + 2 log b a b bằng:
A. 6
B. 7
C. 5
D. 4
Cho a,b là các số thực thỏa mãn log 2 . log 2 a - log b = 2 . Hỏi a,b thỏa mãn hệ thức nào dưới đây?
A. a = 100b
B. a = 100 - b
C. a = =100 + b
D. a = 100 b