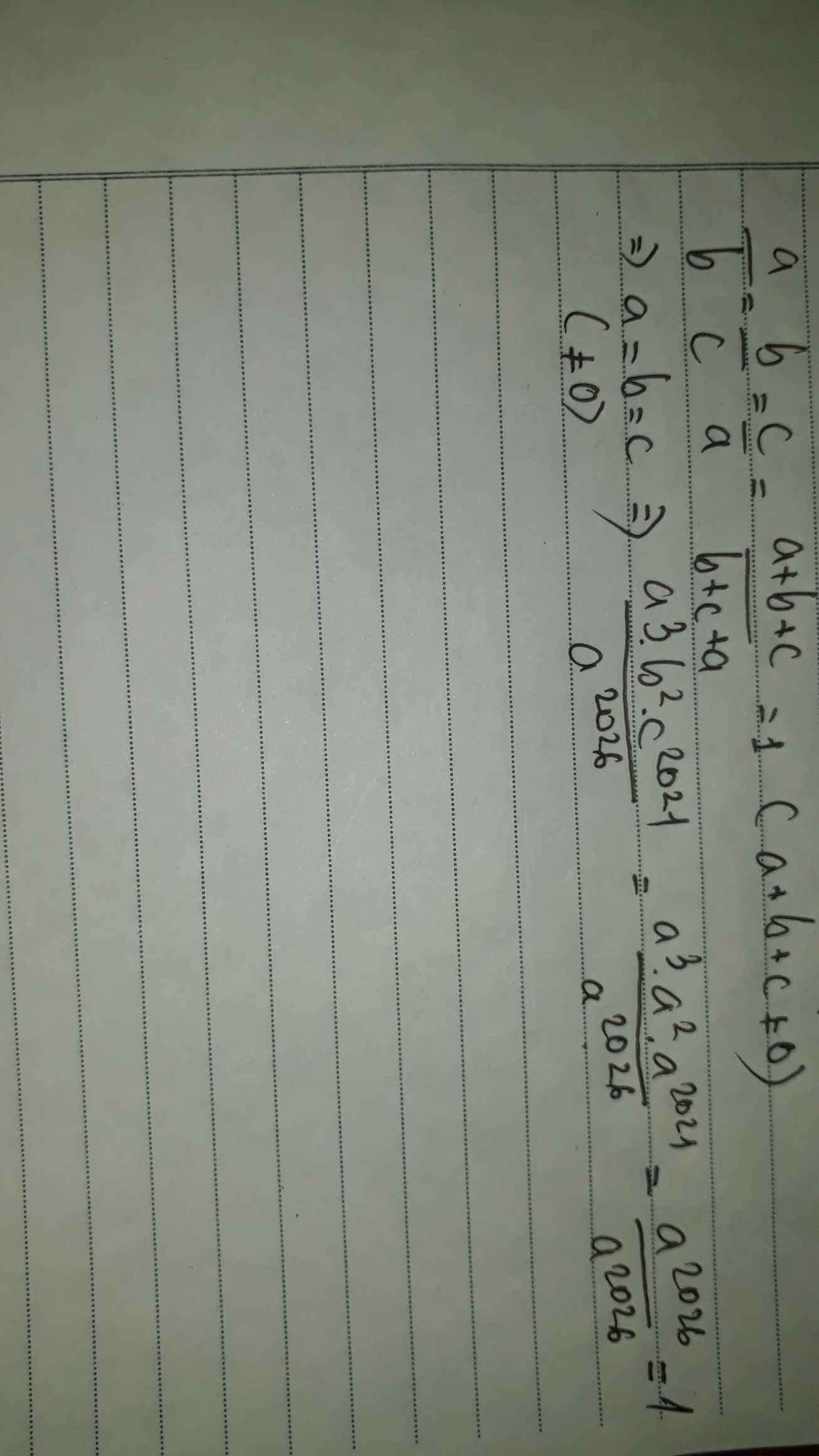Ta có: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\) \(\left(a+b+c\ne0\right)\)
Áp dụng tính chất dãy tỷ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}\)
Mà \(a+b+c\ne0\)
Nên: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=1\\ \Rightarrow a=b=c\)
Thay vào biểu thức \(\dfrac{a^3.b^2.c^{2021}}{a^{2026}}\) ta được:
\(\dfrac{a^3.a^2.a^{2021}}{a^{2026}}=\dfrac{a^{2026}}{a^{2026}}=1\)
Vậy giá trị của \(\dfrac{a^3.b^2.c^{2021}}{a^{2026}}=1\)