Vẽ lại hình:
Ta có: \(\hat{A_1}+\hat{A_2}=180^0\) (hai góc kề bù)
=>\(\hat{A_2}=180^0-60^0=120^0\)
AC//BD
=>\(\hat{A_1}=\hat{B_1}\) (hai góc đồng vị)
=>\(\hat{B_1}=60^0\)
Ta có: \(\hat{B_1}=\hat{B_3}\) (hai góc đối đỉnh)
mà \(\hat{B_1}=60^0\)
nên \(\hat{B_3}=60^0\)
Ta có: AC//BD
=>\(\hat{C_3}=\hat{D_3}\) (hai góc đồng vị)
=>\(\hat{D_3}=130^0\)
Ta có: \(\hat{D_3}=\hat{D_1}\) (hai góc đối đỉnh)
mà \(\hat{D_3}=130^0\)
nên \(\hat{D_1}=130^0\)

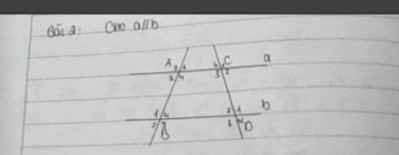 cho A1=60,C3=130 tính A2,B1,B3,D3,D1
cho A1=60,C3=130 tính A2,B1,B3,D3,D1










