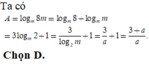Các câu hỏi tương tự
Cho hai số dương a và b. Đặt
X
log
a
+
b
2
,
Y
log
a
+
log
b
2
. Khẳng định nào dưới đây là đúng
Đọc tiếp
Cho hai số dương a và b. Đặt X = log a + b 2 , Y = log a + log b 2 . Khẳng định nào dưới đây là đúng
![]()
![]()
![]()
![]()
Rút gọn biểu thức
A
a
5
3
.
a
7
3
a
4
.
a
-
2...
Đọc tiếp
Rút gọn biểu thức A = a 5 3 . a 7 3 a 4 . a - 2 7 với a>0 ta được kết quả A = a m n trong đó m , n ∈ ℕ * và m n là phân số tối giản. Khẳng định nào sau đây đúng?
![]()
![]()
![]()
![]()
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
Cho
a
-
3
a
-
2
và ax bx. Khẳng định nào sau đây là đúng A. 1 a b 0 B. 1 b a 0 C. a b 1 D. b a 1
Đọc tiếp
Cho a - 3 > a - 2 và ax > bx. Khẳng định nào sau đây là đúng
A. 1 > a > b > 0
B. 1 > b > a > 0
C. a > b > 1
D. b > a > 1
Cho hai số thực a và b, với 0 a 1 b. Khẳng định nào sau đây là đúng? A.
log
b
a
+
log
a
b
0
B.
log
b
a
+
log
a
b
0
C.
log
b
a...
Đọc tiếp
Cho hai số thực a và b, với 0 < a < 1 < b. Khẳng định nào sau đây là đúng?
A. log b a + log a b < 0
B. log b a + log a b = 0
C. log b a + log a b > 0
D. log b a + log a b ≥ 2
Cho hai số thực a và b , với 0 a b 1. Khẳng định nào sau đây là đúng ? A.
log
b
a
1
log
a
b
B.
log
b
a
log
a
b
1
C.
log
a
b...
Đọc tiếp
Cho hai số thực a và b , với 0 < a < b < 1. Khẳng định nào sau đây là đúng ?
A. log b a < 1 < log a b
B. log b a < log a b < 1
C. log a b < 1 < log b a
D. 1 < log a b < log b a
Cho các số thực dương a,b với
a
≠
1
và
log
a
b
0
. Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho các số thực dương a,b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
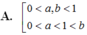
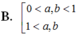
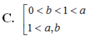
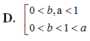
Cho các số thực dương a, b với
a
≠
1
và
log
a
b
0
.
Khẳng định nào sau đây là đúng?
Đọc tiếp
Cho các số thực dương a, b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
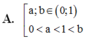
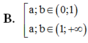
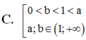
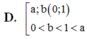
Cho các số thực dương a, b với
a
≠
1
và
log
a
b
0
. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0
a...
Đọc tiếp
Cho các số thực dương a, b với a ≠ 1 và log a b > 0 . Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b .
B. 0 < a , b < 1 1 < a , 1 < b .
C. 0 < b < 1 < a 1 < a , 1 < b .
D. 0 < b , a < 1 0 < a < 1 < b .