Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
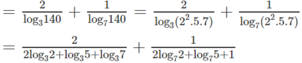
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()
Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
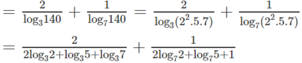
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()
Đặt m = log 2 và n = log 7. Hãy biểu diễn log 6125 7 theo m và n.
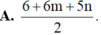
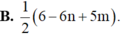
![]()
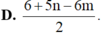
Cho f x = a ln x + x 2 + 1 + b sin x + 6 với a , b ∈ ℝ . Biết rằng f(log(log e)) = 2. Tính giá trị của f(log(ln10)).
A. 10
B. 2
C. 4
D. 8
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Đặt log 3= p và log 5= q Hãy biểu diễn log1530 theo p và q
A. 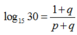
B. 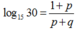
C. 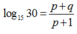
D. 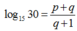
Cho a là số nguyên dương lớn nhất thỏa mãn \(3{\log _3}\left( {1 + \sqrt a + \sqrt[3]{a}} \right) > 2{\log _2}\sqrt a\).Tìm phần nguyên của \({\log _2}\left( {2017a} \right)\)
A.14
B.22
C.16
D.19
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố là:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
Cho log a= 10; log b = 100. Khi đó ![]() bằng
bằng
A. 290
B. 310
C. –290
D. 30
Tính giá trị biểu thức: P = l o g ( t a n 1 o ) + l o g ( t a n 2 o ) + l o g ( t a n 3 o ) + . . . + l o g ( t a n 88 o ) + l o g ( t a n 89 o )
A. 1
B. 0
C. 1 2 log 2
D. 1 2 log 3 2
Tính giá trị của biểu thức S = log 1 2 + log 2 3 = log 3 4 + . . . + log 99 100
A. 1 10
B. - 1 10
C. 2
D. -2
Tính giá trị của biểu thức P = log ( tan 1 0 ) + log ( tan 2 0 ) + log ( tan 3 0 ) + . . . + log ( tan 89 0 ) .
![]()
![]()
![]()
![]()