Các câu hỏi tương tự
Gọi A,B là hai điểm thuộc hai nhánh khác nhau trên đồ thị (C) của hàm số , độ dài ngắn nhất của đoạn thẳng AB là A.4
3
B.2
3
C.
2
3
D.4 B.2
3
C.
2
3
D.4
Đọc tiếp
Gọi A,B là hai điểm thuộc hai nhánh khác nhau trên đồ thị (C) của hàm số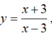 
, độ dài ngắn nhất của đoạn thẳng AB là
A.4 3 B.2 3 C. 2 3 D.4
B.2 3
C. 2 3
D.4
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.
B.
C.
D. 
Đồ thị (C) của hàm số
y
x
+
1
x
-
1
và đường thẳng d: y2x - 1 cắt nhau tại hai điểm A và B khi đó độ dài đoạn AB bằng? A. . B. . C. . D. .
Đọc tiếp
Đồ thị (C) của hàm số y = x + 1 x - 1 và đường thẳng d: y=2x - 1 cắt nhau tại hai điểm A và B khi đó độ dài đoạn AB bằng?
A. 
.
B. 
.
C. 
.
D. 
.
Cho hàm số
y
x
-
1
x
+
2
có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận của (C) . Xét tam giác đều ABI có hai đỉnh A; B thuộc (C) , đoạn thẳng AB có độ dài bằng A.
6
.
B.
2
3
.
C. 2. D.
2
2...
Đọc tiếp
Cho hàm số y = x - 1 x + 2 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận của (C) . Xét tam giác đều ABI có hai đỉnh A; B thuộc (C) , đoạn thẳng AB có độ dài bằng
A. 6 .
B. 2 3 .
C. 2.
D. 2 2 .
Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C):
y
x
+
2
x
-
1
sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB. A. B. C. D.
Đọc tiếp
Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C): y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A.
B. 
C. 
D. 
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN. A. B. MN 3 C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng chỉ có đúng hai điểm thuộc đồ thị (C) cách đều hai trục tọa độ. Gọi các điểm đó lần lượt là M và N. Tính độ dài đoạn thẳng MN.
A.
B. MN = 3
C. 
D. 
Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số y
2
x
x
-
1
sao cho tam giác ABC vuông cân tại đỉnh A(2; 0), khi đó giá trị biểu thức Tab+cd bằng: A. 6 B. 0 C. -9 D. 8
Đọc tiếp
Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số y = 2 x x - 1 sao cho tam giác ABC vuông cân tại đỉnh A(2; 0), khi đó giá trị biểu thức T=ab+cd bằng:
A. 6
B. 0
C. -9
D. 8
Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số
y
2
x
x
-
1
sao cho tam giác ABC vuông cân tại đỉnh A(2; 0), khi đó giá trị biểu thức Tab + cd bằng: A. 6 B. 0 C. -9 D. 8
Đọc tiếp
Biết hai điểm B(a; b), C(c; d) thuộc hai nhánh của đồ thị hàm số y = 2 x x - 1 sao cho tam giác ABC vuông cân tại đỉnh A(2; 0), khi đó giá trị biểu thức T=ab + cd bằng:
A. 6
B. 0
C. -9
D. 8
Cho (C) là đồ thị của hàm số
y
x
-
3
x
+
1
Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN. A. I(-1;1) B.I(0;-3/2) C.I(0;3/2) D. I(-2;2)
Đọc tiếp
Cho (C) là đồ thị của hàm số y = x - 3 x + 1 Biết rằng, chỉ có hai điểm thuộc đồ thị (C) cách đều hai điểm A(2;0) và B(0;-2). Gọi các điểm đó lần lượt là M và N. Tìm tọa độ trung điểm I của đoạn thẳng MN.
A. I(-1;1)
B.I(0;-3/2)
C.I(0;3/2)
D. I(-2;2)