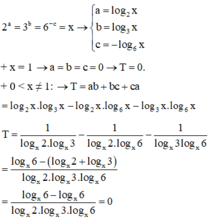Các câu hỏi tương tự
Cho a, b, c là các số thực thỏa mãn
2
a
3
b
6
−
c
. Giá trị của biểu thức
T
a
b
+
b
c
+
c
a
bằng bao nhiêu A. T 3. B. T 2. C. T 1. D. T 0.
Đọc tiếp
Cho a, b, c là các số thực thỏa mãn 2 a = 3 b = 6 − c . Giá trị của biểu thức T = a b + b c + c a bằng bao nhiêu
A. T = 3.
B. T = 2.
C. T = 1.
D. T = 0.
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn
a
−
3
2
+
b
−
6
2
1
v
à
4
c
+
3
d
−
5
0
. Tính giá trị nhỏ nhất của
T...
Đọc tiếp
Cho các số thực a, b, c, d thay đổi luôn thỏa mãn a − 3 2 + b − 6 2 = 1 v à 4 c + 3 d − 5 = 0 . Tính giá trị nhỏ nhất của T = c − a 2 + d − b 2
A. 16
B. 18
C. 9
D. 15
Cho a,b,c là các số thực dương thỏa mãn
a
log
5
2
4
,
b
log
4
6
1
,
log
,
c
log
7
3
49
Tính giá trị của biểu thức
T
a...
Đọc tiếp
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Cho a, b, c là các số thực dương khác 1 và thỏa mãn
a
log
3
7
27
,
b
l
o
g
7
11
49
,
c
log
11
25
11
.
Tính giá trị của biểu t...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1 và thỏa mãn a log 3 7 = 27 , b l o g 7 11 = 49 , c log 11 25 = 11 . Tính giá trị của biểu thức T = a log 3 2 7 + b l o g 7 2 11 + c log 11 2 25
A. T=469
B. T=3141
C. T=2017
D. T = 76 + 11
Cho các số thực a, b, c thỏa mãn
a
log
3
7
2
27
;
b
log
7
11
2
49
;
c
log
11...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn a log 3 7 2 = 27 ; b log 7 11 2 = 49 ; c log 11 25 2 = 11 . Tính giá trị của biểu thức T = a log 3 7 2 + b log 7 11 2 + c log 11 25 2
A. T = 496
B. T = 649
C. T = 469
D. T = 694
Cho các số thực a, b thỏa mãn 1ab và
log
a
b
+
log
b
a
2
3
. Tính giá trị của biểu thức
T
log
a
b
a
2
+
b
2
A.
1...
Đọc tiếp
Cho các số thực a, b thỏa mãn 1<a<b và log a b + log b a 2 = 3 . Tính giá trị của biểu thức T = log a b a 2 + b 2
A. 1 6
B. 3 2
C. 6
D. 2 3
Cho các số thực a, b thỏa mãn 1 a b và
log
a
b
+
log
b
a
2
3
. Tính giá trị của biểu thức
T
log
a
b
a
2
+
b
2
A.
1...
Đọc tiếp
Cho các số thực a, b thỏa mãn 1< a < b và log a b + log b a 2 = 3 . Tính giá trị của biểu thức T = log a b a 2 + b 2
A. 1 6
B. 3 2
C. 6
D. 2 3
Cho các số thực a, b thỏa mãn
2
5
a
b
1
. Tìm giá trị nhỏ nhất của biểu thức
T
27
log
a
b
2
b
+
log
b
8
5
a
−
2...
Đọc tiếp
Cho các số thực a, b thỏa mãn 2 5 < a < b < 1 . Tìm giá trị nhỏ nhất của biểu thức T = 27 log a b 2 b + log b 8 5 a − 2 25 − 3.
A. 11
B. 8
C. 9
D. 6
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4