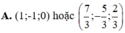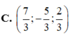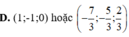a.
\(\overrightarrow{AC}=\left(4;-3;-2\right)\)
Gọi \(K\left(x;y;z\right)\Rightarrow\overrightarrow{BK}=\left(x-1;y-2;z+2\right)\)
\(\overrightarrow{BK}=3\overrightarrow{AC}\Rightarrow\left\{{}\begin{matrix}x-1=3.4=12\\y-1=3.\left(-3\right)=-9\\z+2=3.\left(-2\right)=-6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=13\\y=-8\\z=-8\end{matrix}\right.\) \(\Rightarrow K\left(13;-8;-8\right)\)
b,
Gọi \(N\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{NB}=\left(1-x;2-y;-2-z\right)\\\overrightarrow{NC}=\left(-x;-2-y;1-z\right)\end{matrix}\right.\)
\(\overrightarrow{NB}=-3\overrightarrow{NC}\Rightarrow\left\{{}\begin{matrix}1-x=3x\\2-y=6+y\\-2-z=-3+z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=-2\\z=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow N\left(\dfrac{1}{4};-2;\dfrac{1}{2}\right)\)
c.
M thuộc Oz nên tọa độ dạng \(M\left(0;0;z\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(4;-1;z-3\right)\)
Tam giác ACM vuông tại A \(\Rightarrow\overrightarrow{AM}.\overrightarrow{AC}=0\)
\(\Rightarrow4.4+\left(-1\right).\left(-3\right)-2\left(z-3\right)=0\Rightarrow z=\dfrac{25}{2}\)
\(\Rightarrow M\left(0;0;\dfrac{25}{2}\right)\)
d.
P thuộc Oyz nên tọa độ dạng \(P\left(0;y;z\right)\)
\(\Rightarrow\overrightarrow{AP}=\left(4;y-1;z-3\right)\)
A,C,P thẳng hàng khi 2 vecto \(\overrightarrow{AC};\overrightarrow{AP}\) cùng phương
\(\Rightarrow\dfrac{4}{4}=\dfrac{y-1}{-3}=\dfrac{z-3}{-2}\Rightarrow\left\{{}\begin{matrix}y=-2\\z=1\end{matrix}\right.\)
\(\Rightarrow P\left(0;-2;1\right)\)