Cho 4 điểm A; B; C; S không đồng phẳng. Gọi I và H lần lượt là trung điểm của SA và AB. Trên SC lấy điểm K sao cho IK không song song với AC ( K không trùng với các đầu mút). Gọi E là giao điểm của BC và (IHK). Tìm mệnh đề đúng
A. E nằm trên tia đối của tia BC
B. E nằm trên tia đối của tia CB
C. E nằm giữa C và B
D. Tất cả sai
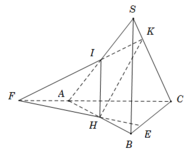
+ Chọn mặt phẳng phụ (ABC) chứa BC.
+ Tìm giao tuyến của hai mặt phẳng (ABC) và (IHK) .
Ta có H là điểm chung thứ nhất của (ABC ) và (IHK) .
Trong mặt phẳng (SAC) do IK không song song với AC nên gọi giao điểm của IK và CA là F. Ta có
- F thuộc AC mà A C ⊂ A B C nên F ∈ A B C
- F thuộc IK mà I K ⊂ I H K nên F ∈ I H K
Suy ra F là điểm chung thứ hai của (ABC) và (IHK) .
Do đó giao tuyến của (ABC) và (IHK) là HF.
+ Trong mặt phẳng (ABC) , gọi giao điểm HF và BC là E. Ta có
▪ E thuộc HF mà H F ⊂ I H K → E ∈ I H K
▪E thuộc BC.
Vậy giao điểm của BC và (IHK) là E.
Chọn C





