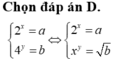Các câu hỏi tương tự
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Tìm tất cả các giá trị của m để đường thẳng d: yx+4 cắt đồ thị hàm số
y
x
3
+
2
m
x
2
+
m
+
3
x
+
4
tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3) A.
m...
Đọc tiếp
Tìm tất cả các giá trị của m để đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + m + 3 x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = − 3 m = − 2
Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(2;4;-1), B(1;4;-1), C(2;4;3), D(2;2;-1), biết M(x;y;z) để
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
đạt giá trị nhỏ nhất thì x+y+z bằng A. 6 B.
21
4
C. 8 D. 9
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(2;4;-1), B(1;4;-1), C(2;4;3), D(2;2;-1), biết M(x;y;z) để M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất thì x+y+z bằng
A. 6
B. 21 4
C. 8
D. 9
Trong không gian Oxyz cho A(0;1;1), B(2;-1;1), C(4;1;1) và (P): x+y+z-60. Xét điểm M(a;b;c) thuộc mp (P) sao cho
M
A
→
+
2
M
B
→
+
M
C
→...
Đọc tiếp
Trong không gian Oxyz cho A(0;1;1), B(2;-1;1), C(4;1;1) và (P): x+y+z-6=0. Xét điểm M(a;b;c) thuộc mp (P) sao cho M A → + 2 M B → + M C → đạt giá trị nhỏ nhất. Giá trị của 2a+4b+c bằng
A. 6
B. 12
C. 7
D. 5
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho các số thực a, b, c 0 và a, b, c khác 1, thỏa mãn
log
a
b
2
x
,
log
b
2
c
y
. Giá trị của
log
c
a
bằng A.
2
x
y
B. 2...
Đọc tiếp
Cho các số thực a, b, c > 0 và a, b, c khác 1, thỏa mãn log a b 2 = x , log b 2 c = y . Giá trị của log c a bằng
A. 2 x y
B. 2xy
C. 1 2 x y
D. x y 2
Trong không gian Oxyz, cho ba điểm A(3;5;-1), B(7;x;1), C(9;2;y). Để A, B, C thẳng hàng thì giá trị x+y bằng
A. 5
B. 6
C. 4
D. 7
Tính tổng tất cả các giá trị của m biết đồ thị hàm số
y
x
3
-
2
mx
2
+
(
m
+
2
)
x
+
4
và đường thẳng y x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng
8
2
với I(1;3) A.3 B. 8 C. 1 D. 5
Đọc tiếp
Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x 3 - 2 mx 2 + ( m + 2 ) x + 4 và đường thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng 8 2 với I(1;3)
A.3
B. 8
C. 1
D. 5
Cho hàm số y
3
x
+
b
ax
-
2
(
ab
≠
-
2
)
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x + y -40. Khi đó giá trị của a-3b bằng:...
Đọc tiếp
Cho hàm số y= 3 x + b ax - 2 ( ab ≠ - 2 ) . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x + y -4=0. Khi đó giá trị của a-3b bằng:
A. -2
B. 4
C. 5
D. -1