g) \(\left(4^{2x}-1\right)^2=5^2.9\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}-1=5.3\\4^{2x}-1=-5.3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}=16\\4^{2x}=-14\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow4^{2x}=4^2\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
h) \(2^{x+1}+2^{x+2}+2^{x+3}+...+2^{x+101}=2^{104}-8\)
\(\Leftrightarrow2^{x+1}\left(1+2+2^2+...+2^{100}\right)=2^{104}-8\)
\(\Leftrightarrow2^{x+1}.\left(2^{101}-1\right)=2^{104}-2^3\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^{104}-2^3}{2^{101}-1}\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^3\left(2^{101}-1\right)}{2^{101}-1}\)
\(\)\(\Leftrightarrow2^{x+1}=2^3\)
\(\Leftrightarrow x+1=3\)
\(\Leftrightarrow x=2\)

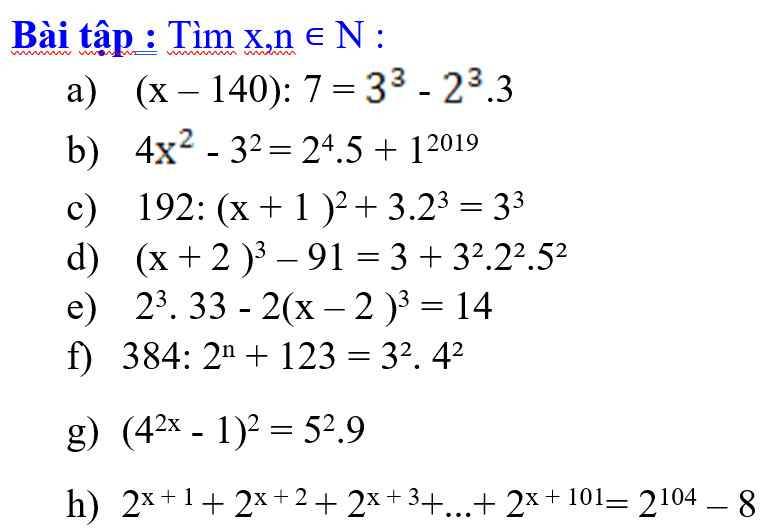








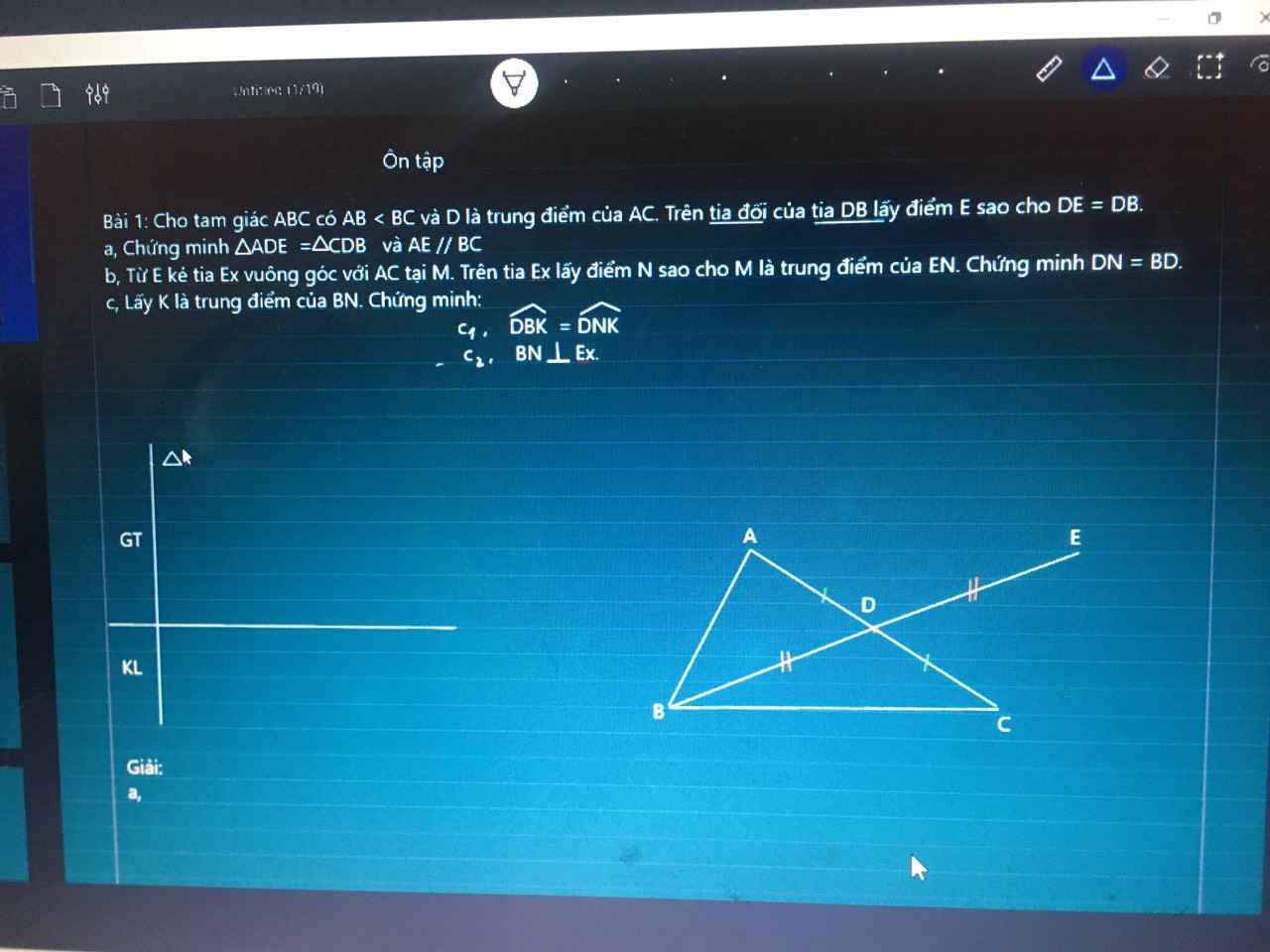


 Chỉ mik câu d với
Chỉ mik câu d với