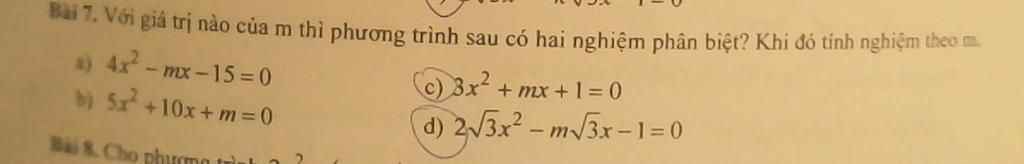c: Để phương trình có hai nghiệm phân biệt thì Δ>0
=>\(m^2-4\cdot3\cdot1>0\)
=>\(m^2>12\)
=>\(\left[{}\begin{matrix}m>2\sqrt{3}\\m< -2\sqrt{3}\end{matrix}\right.\)
Phương trình sẽ có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{-m-\sqrt{m^2-12}}{2\cdot3}=\dfrac{-m-\sqrt{m^2-12}}{6}\\x=\dfrac{-m+\sqrt{m^2-12}}{6}\end{matrix}\right.\)
d: Để phương trình có hai nghiệm phân biệt thì Δ>0
=>\(\left(-m\sqrt{3}\right)^2-4\cdot2\sqrt{3}\cdot\left(-1\right)>0\)
=>\(3m^2+8\sqrt{3}>0\)(luôn đúng)
=>Phương trình luôn có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{m\sqrt{3}-\sqrt{3m^2+8\sqrt{3}}}{2\cdot2\sqrt{3}}=\dfrac{3m-\sqrt{9m^2+24\sqrt{3}}}{12}\\x_2=\dfrac{3m+\sqrt{9m^2+24\sqrt{3}}}{12}\end{matrix}\right.\)