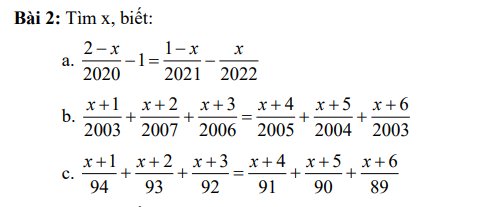\(c,\dfrac{x+1}{94}+\dfrac{x+2}{93}+\dfrac{x+3}{92}=\dfrac{x+4}{91}+\dfrac{x+5}{90}+\dfrac{x+6}{89}\\ =>\left(\dfrac{x+1}{94}+1\right)+\left(\dfrac{x+2}{93}+1\right)+\left(\dfrac{x+3}{92}+1\right)=\left(\dfrac{x+4}{91}+1\right)+\left(\dfrac{x+5}{90}+1\right)+\left(\dfrac{x+6}{89}+1\right)\\ =>\dfrac{x+95}{94}+\dfrac{x+95}{93}+\dfrac{x+95}{92}=\dfrac{x+95}{91}+\dfrac{x+95}{90}+\dfrac{x+95}{89}\\ =>\dfrac{x+95}{94}+\dfrac{x+95}{93}+\dfrac{x+95}{92}-\dfrac{x+95}{91}-\dfrac{x+95}{90}-\dfrac{x+95}{89}=0\\ =>\left(x+95\right)\left(\dfrac{1}{94}+\dfrac{1}{93}+\dfrac{1}{92}-\dfrac{1}{91}-\dfrac{1}{90}-\dfrac{1}{89}\right)=0\\ =>x+95=0\\ =>x=-95\)\(a,\dfrac{2-x}{2020}-1=\dfrac{1-x}{2021}-\dfrac{x}{2022}\\ =>\dfrac{2-x}{2020}-1+2=\left(\dfrac{1-x}{2021}+1\right)-\left(\dfrac{x}{2022}-1\right)\\ =>\dfrac{2-x+2020}{2020}=\dfrac{1-x+2021}{2021}-\dfrac{x-2022}{2022}\\ =>\dfrac{2022-x}{2020}=\dfrac{2022-x}{2021}-\dfrac{x-2022}{2022}\\ =>\dfrac{2022-x}{2020}-\dfrac{2022-x}{2021}-\dfrac{2022-x}{2022}=0\\ =>\left(2022-x\right)\left(\dfrac{1}{2020}-\dfrac{1}{2021}-\dfrac{1}{2022}\right)=0\\ =>2022-x=0\\ =>x=2022\)
\(b,\dfrac{x+1}{2008}+\dfrac{x+2}{2007}+\dfrac{x+3}{2006}=\dfrac{x+4}{2005}+\dfrac{x+5}{2004}+\dfrac{x+3}{2006}\\ =>\left(\dfrac{x+1}{2008}+1\right)+\left(\dfrac{x+2}{2007}+1\right)+\left(\dfrac{x+3}{2006}+1\right)=\left(\dfrac{x+4}{2005}+1\right)+\left(\dfrac{x+5}{2004}+1\right)+\left(\dfrac{x+6}{2003}+1\right)\\ =>\dfrac{x+2009}{2008}+\dfrac{x+2009}{2007}+\dfrac{x+2009}{2006}=\dfrac{x+2009}{2005}+\dfrac{x+2009}{2004}+\dfrac{x+2009}{2003}\\ =>\dfrac{x+2009}{2008}+\dfrac{x+2009}{2007}+\dfrac{x+2009}{2006}-\dfrac{x+2009}{2005}-\dfrac{x+2009}{2004}-\dfrac{x+2009}{2003}=0\\ =>\left(x+2009\right)\left(\dfrac{1}{2008}+\dfrac{1}{2007}+\dfrac{1}{2006}-\dfrac{1}{2005}-\dfrac{1}{2004}-\dfrac{1}{2003}\right)=0\\ =>x+2009=0\\ =>x=-2009\)