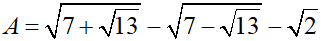\(A=\dfrac{1}{\sqrt{2}}\sqrt{14+2\sqrt{13}}-\dfrac{1}{\sqrt{2}}\sqrt{14-2\sqrt{13}}-\sqrt{2}\)
\(=\dfrac{1}{\sqrt{2}}\sqrt{\left(\sqrt{13}+1\right)^2}-\dfrac{1}{\sqrt{2}}\sqrt{\left(\sqrt{13}-1\right)^2}-\sqrt{2}\)
\(=\dfrac{\sqrt{13}+1}{\sqrt{2}}-\dfrac{\sqrt{13}-1}{\sqrt{2}}-\sqrt{2}\)
\(=\dfrac{2}{\sqrt{2}}-\sqrt{2}=\sqrt{2}-\sqrt{2}=0\)