TK
a) Xét \(\Delta ABH\) và \(\Delta AHC\) có:
\(\widehat{AHB}=\widehat{AHC}\left(AH\perp BC\right)\)
AB=AC (\(\Delta ABC\) cân)
\(\widehat{ABH}=\widehat{ACH}\) (\(\Delta ABC\) cân)
Vậy \(\Delta ABH\) = \(\Delta AHC\) ( cạnh huyền - góc nhọn )
b)
Ta có \(\widehat{EAH}=\widehat{FAH}\) (\(\Delta ABH=\Delta AHC\))
Xét \(\Delta AEH\) và \(\Delta AFH\) có:
\(\widehat{AEH}=\widehat{AFH}\left(HE\perp AB;HF\perp AC\right)\)
AH chung
\(\widehat{EAH}=\widehat{FAH}\left(CMT\right)\)
Vậy \(\Delta AEH=\Delta AFH\) ( cạnh huyền - góc nhọn )
=> HE = HF( 2 cạnh tương ứng)
=> HE = HF (đpcm)
TK
c) Gọi O là giao điểm EF và AH
Ta có: AE = AF (\(\Delta AEH=\Delta AFH\))
Xét \(\Delta AEOvà\Delta AFO\) có:
AE = AF (cmt)
\(\widehat{EAO}=\widehat{FAO}\) ( cm câu b)
AO chung
Vậy \(\Delta AEO=\Delta AFO\left(c-g-c\right)\)
=> EO = OF ( 2 cạnh tương ứng) (1)
=> \(\widehat{AOE}=\widehat{AOF}\) ( 2 góc tương ứng)
Mà 2 góc này nằm ở vị trí kề bù.
=> \(2\widehat{EAO}=180^o\)
=> \(\widehat{EAO}=90^o\)
=> \(AO\perp EF\) (2)
Qua A chỉ kẻ đc một đường thẳng. (3)
Từ (1); (2) và (3)
=> AH là đường trung trực của EF







 giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ
giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ






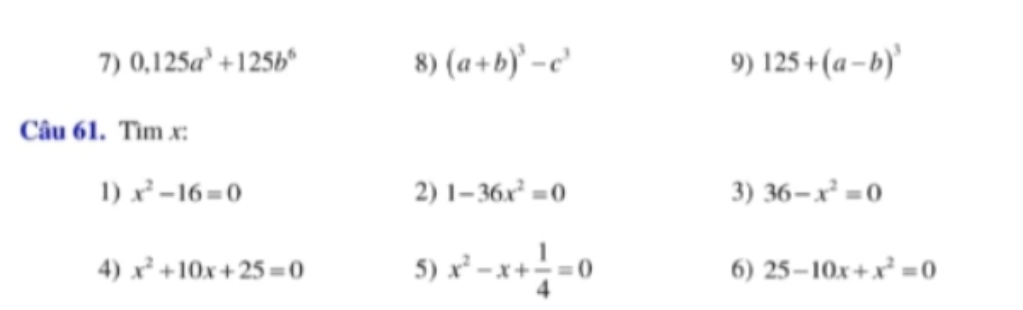



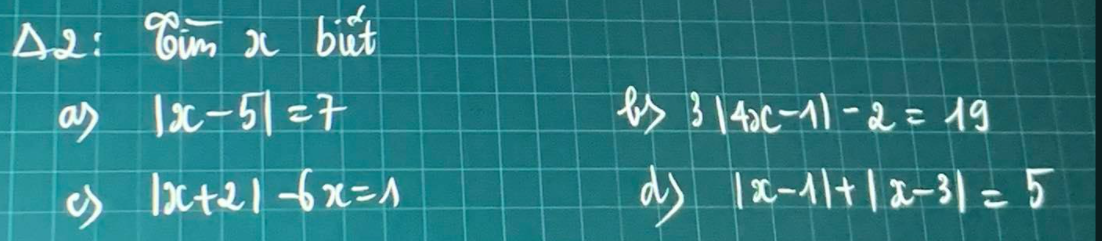 giúp mình 4 câu này nhanh ạ
giúp mình 4 câu này nhanh ạ