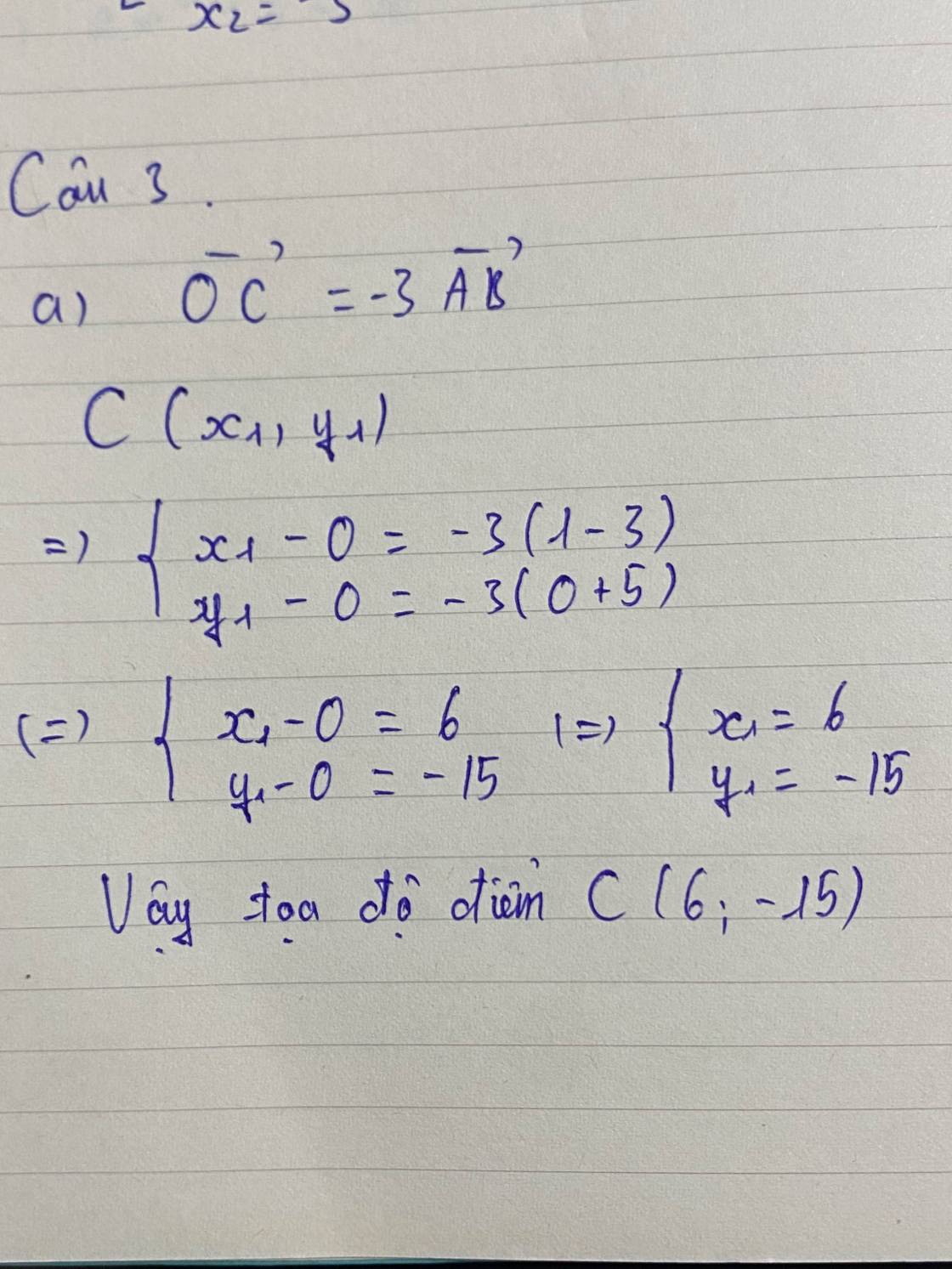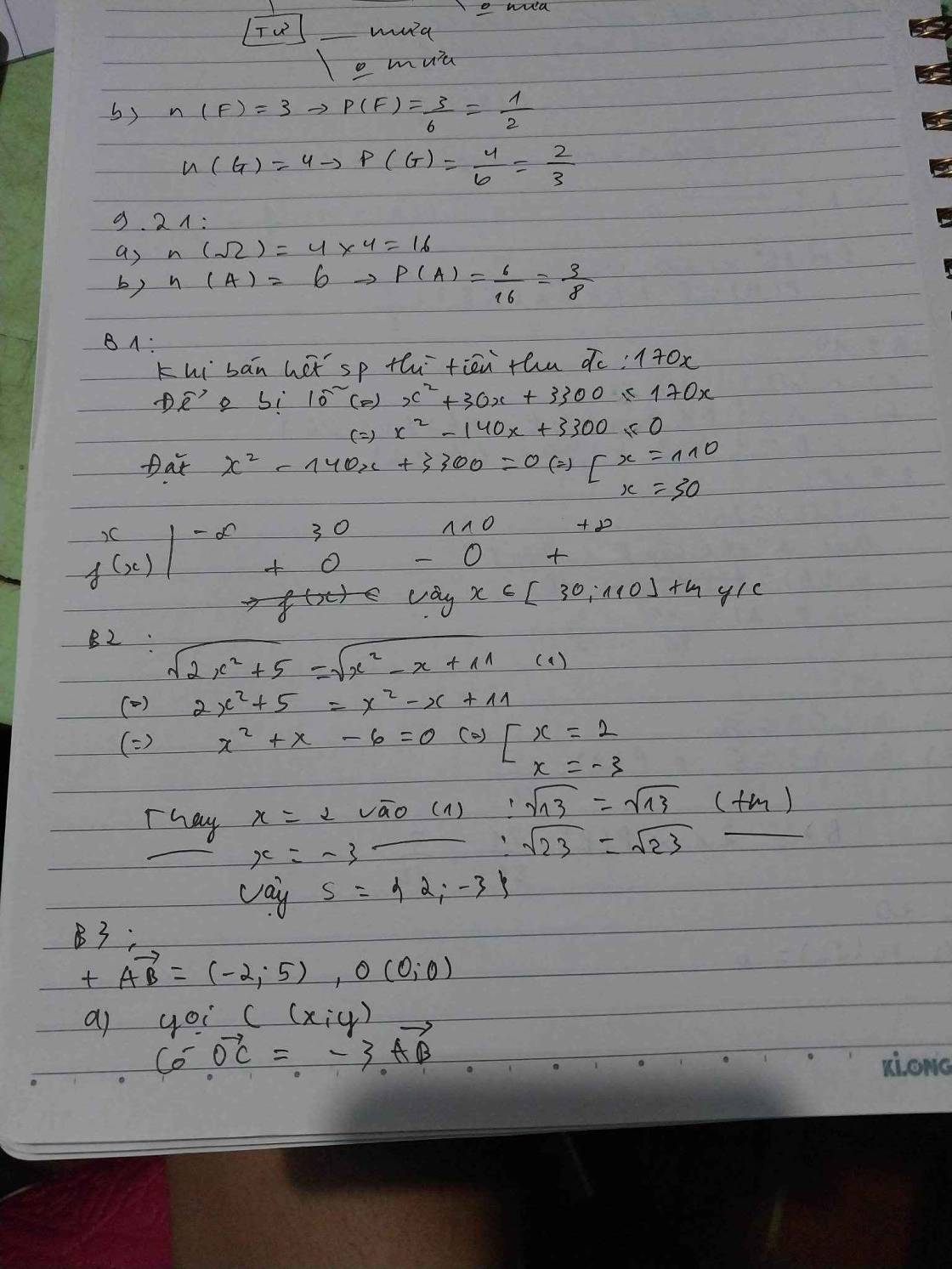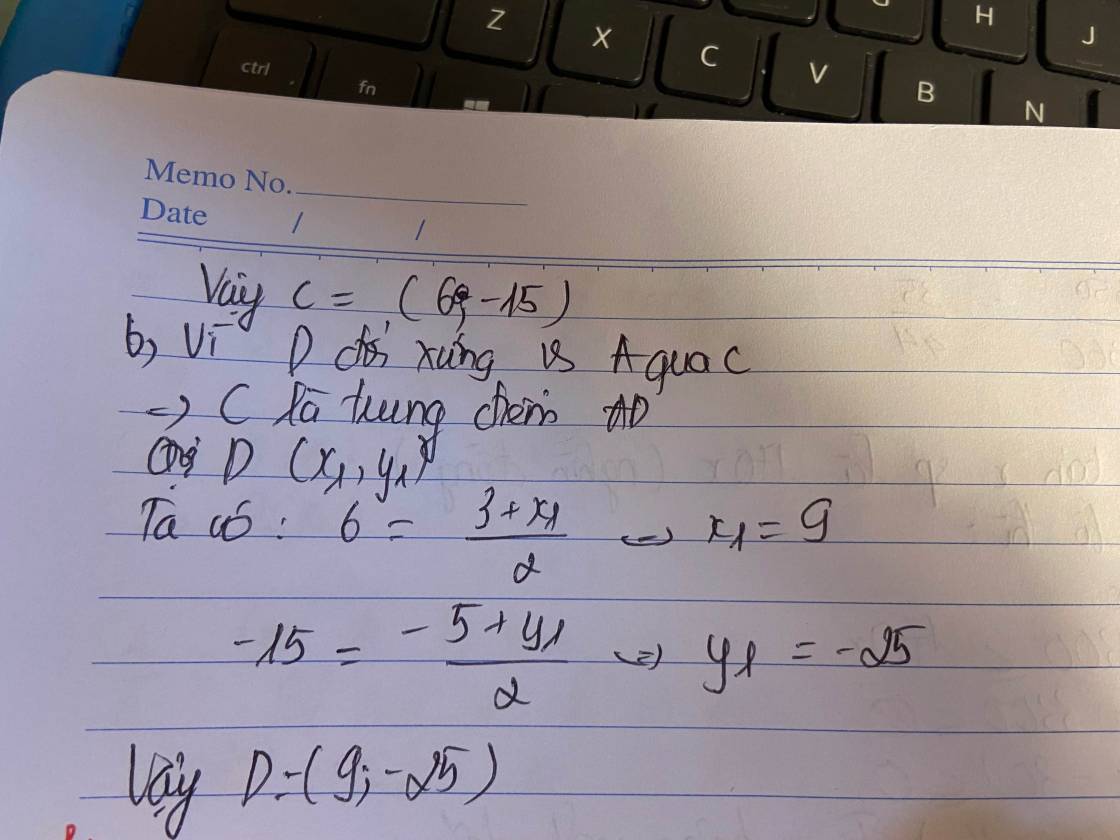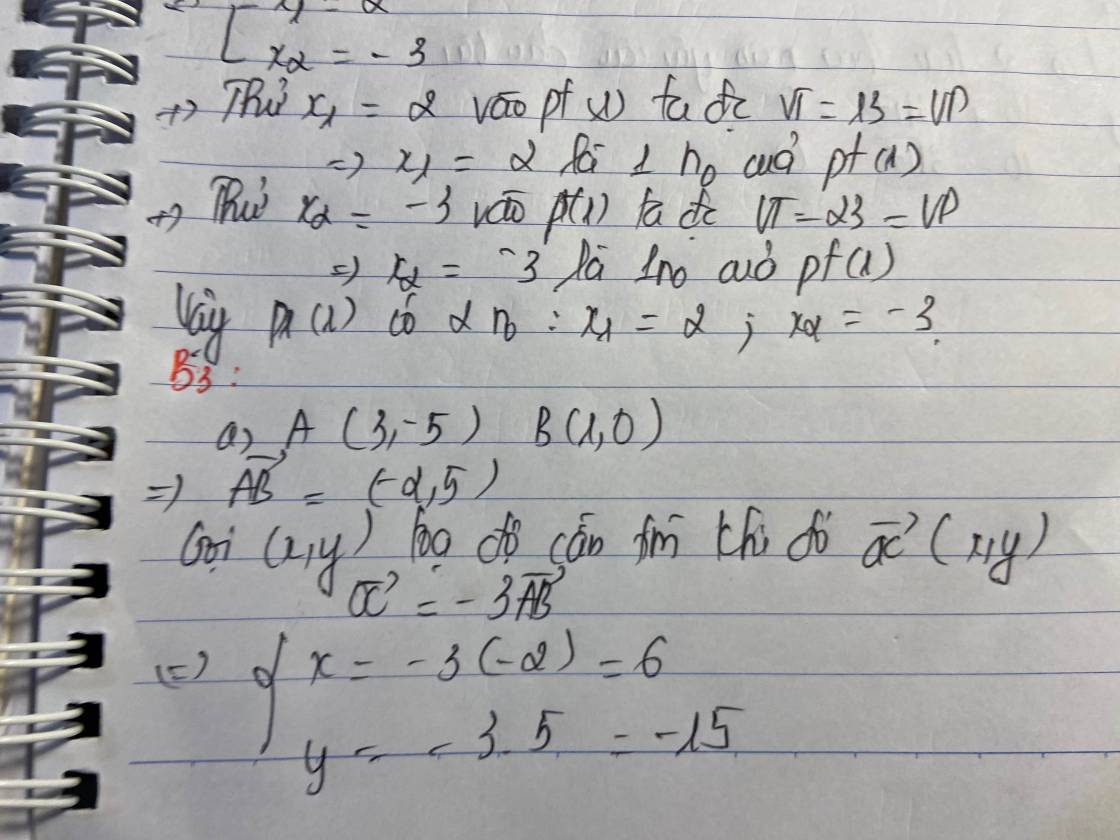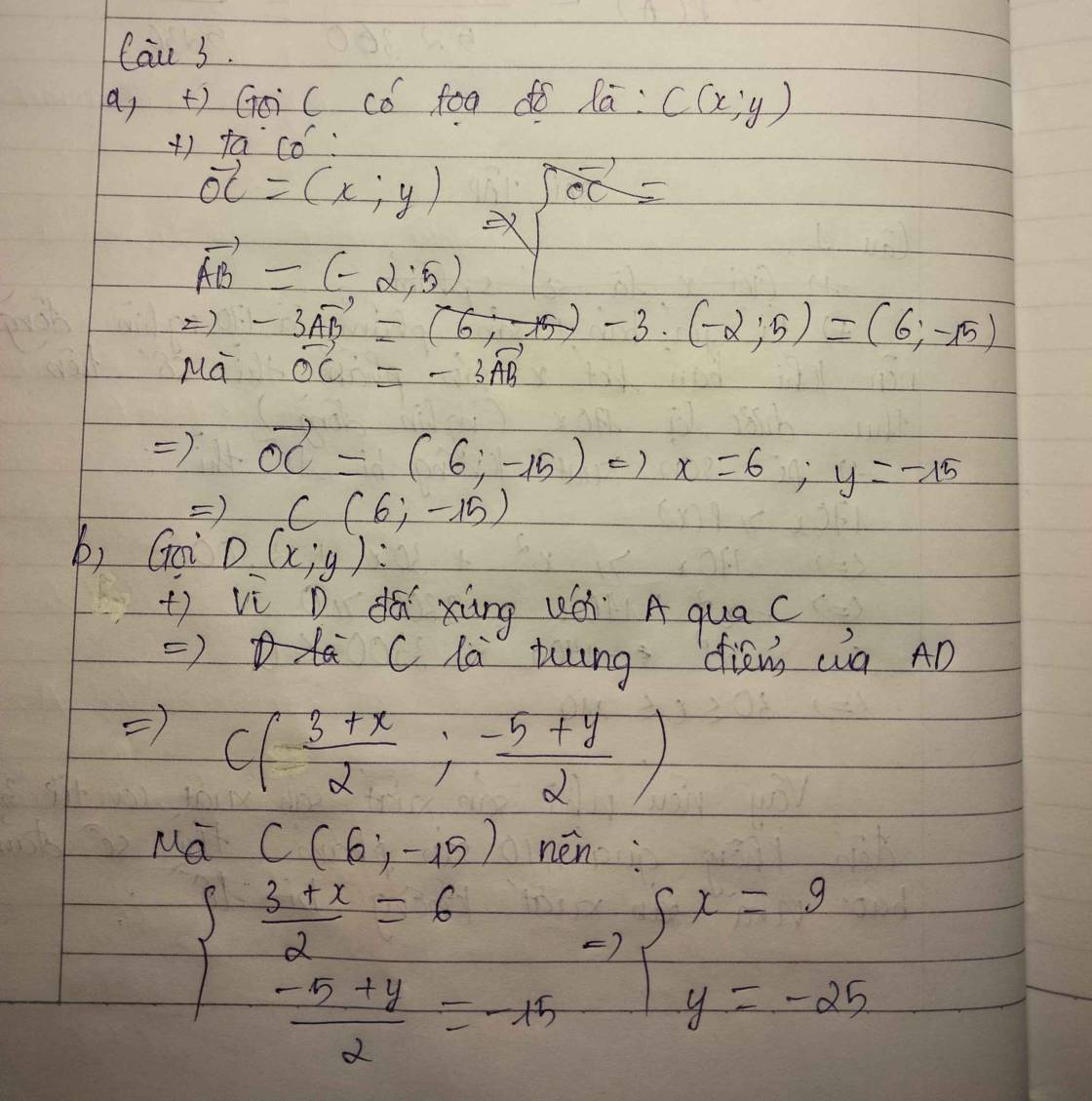a) A(3;-5) ; B(1;0)
=> \(\overrightarrow{AB}\left(-2;5\right)\)
Gọi C(x;y) tọa độ cần tìm
khi đó \(\overrightarrow{OC}\left(x;y\right)\)
\(\overrightarrow{OC}=-3\overrightarrow{AB}\Leftrightarrow\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5=-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(6=\dfrac{3+x_1}{2}\Leftrightarrow x_1=9\)
\(-15=\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)
a) A(3;-5) ; B(1;0)
=> véc tơ AB (−2;5)Gọi C(x;y) tọa độ cần tìm
khi đóvéc tơ OC = -3véc tơ AB <=>\(\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(\dfrac{3+x_1}{2}\)
-15=\(\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)
a) A(3;-5) ; B(1;0)
=> véc tơ AB (−2;5)Gọi C(x;y) tọa độ cần tìm
khi đóvéc tơ OC = -3véc tơ AB <=>\(\left\{{}\begin{matrix}x=-3.\left(-2\right)=6\\y=-3.5-15\end{matrix}\right.\)
Vậy C(6;-15)
b) D đối xứng với A qua C
=> C trung điểm AD
Gọi D(x1;y1)
Ta có : \(\dfrac{3+x_1}{2}\)
-15=\(\dfrac{-5+y_1}{2}\) <=> y1 = -25
Vậy D(9;-25)
C(xc;yc)
ta co OC=(xc;yc),AB=(-2;5) ==>-3AB = (6;-15)
OC-3AB <=> xc=6 ; yc=-15
D doi xung A qua C hay C la trung diem AD <=> {xc= xa+xd/2
{yc=ya+yd/2
<=> xd=2xc-xa=2.6-3=9
<=>yd-ya=2=(-15) - (-5) =-25
==> D(9;-25)