câu 1
a) \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
b) \(B=\sqrt{14+4\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
câu 2 trong mặt phẳng tọa độ 0xy cho đường thẳng (d1): y=2x và đường thẳng (d2): y=-x+2
a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ
b) cho đường thẳng (d3): y=ax+b. xác định a,b biết rằng đường thẳng (d3) song song với đường thẳng (d2), đồng thời cắt đường thẳng (d1) tại điểm có hoành độ bằng 1
Câu 1:
a: \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
\(=4\cdot2\sqrt{6}-3\cdot3\sqrt{6}+5\sqrt{6}-5\sqrt{6}\)
\(=8\sqrt{6}-9\sqrt{6}=-\sqrt{6}\)
b: \(B=\sqrt{14+4\cdot\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
\(=\sqrt{10+2\cdot\sqrt{10}\cdot2+4}-\dfrac{\left(\sqrt{10}-3\right)}{10-9}\)
\(=\sqrt{\left(\sqrt{10}+2\right)^2}-\sqrt{10}+3\)
\(=\sqrt{10}+2-\sqrt{10}+3=5\)
Câu 2:
a:
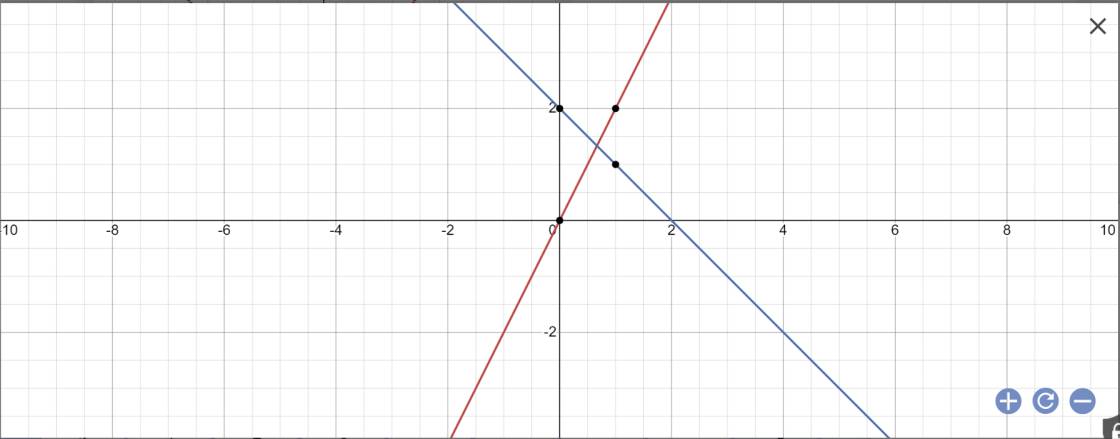
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
vậy: (d3): y=-x+3










