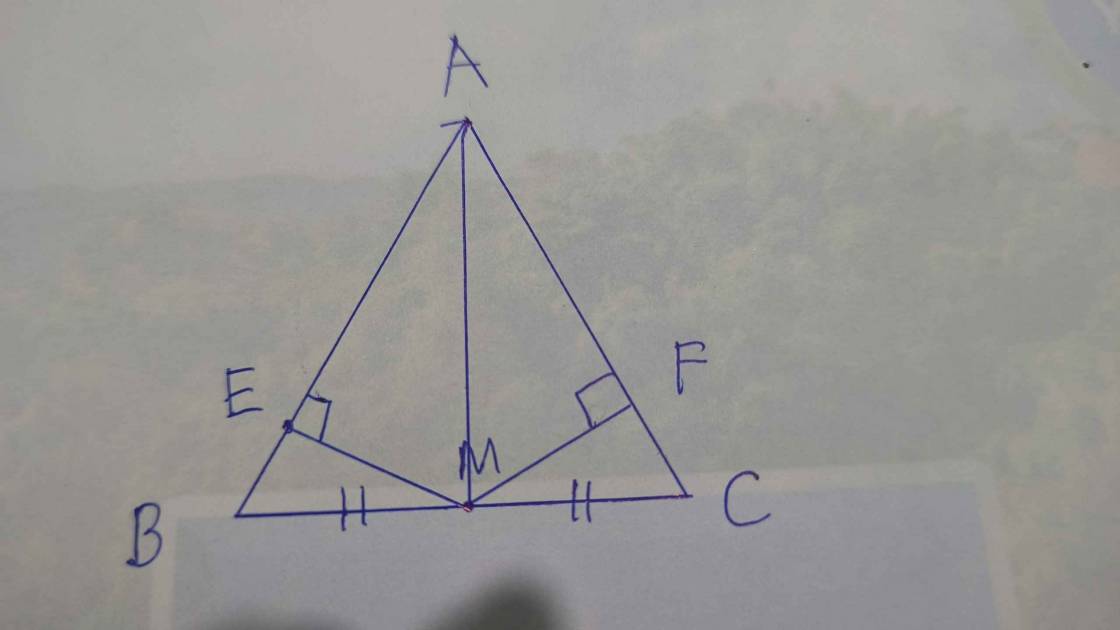ngay chỗ câu b em lộn xíu, EA = FA (2 cạnh tương ứng)
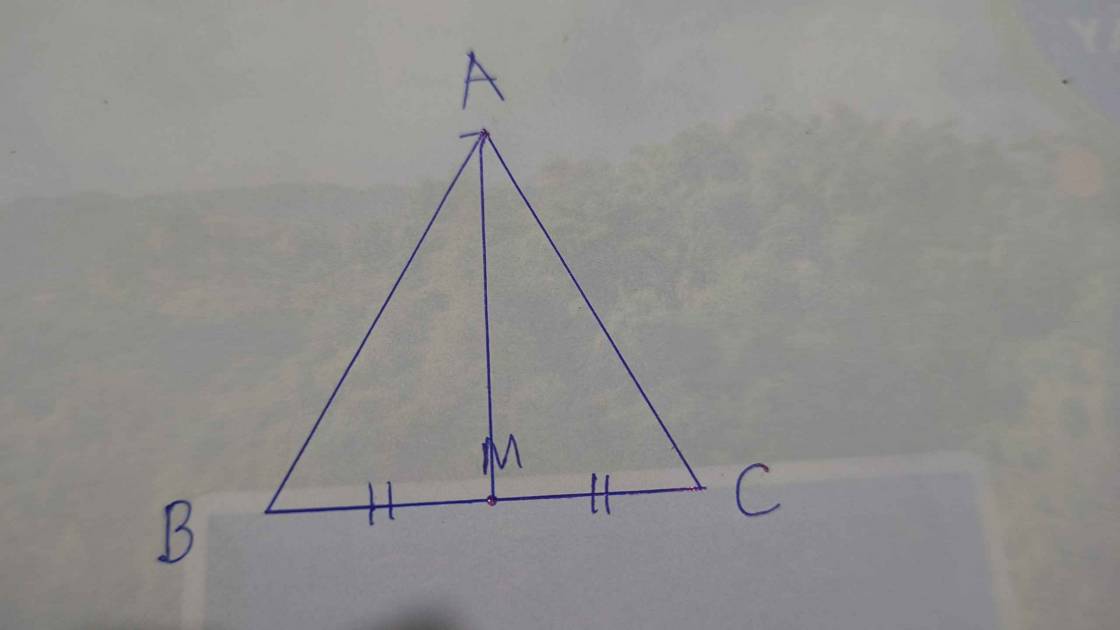
a, c/m và AMBC.
b,Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. c/m : MD = ME.
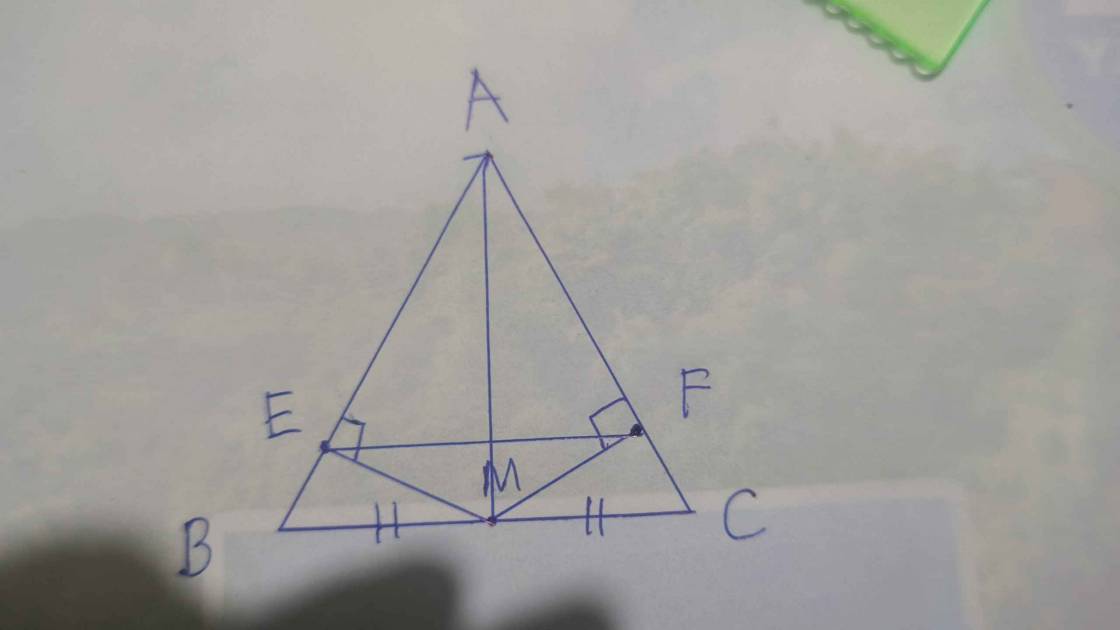
c, Gọi N là trung điểm của DB . Trên tia đối của tia NM lấy điểm K . sao cho NK = NM. Chứng minh các điểm K, D, E thẳng hàng.
a) Xét Δ AMB và △ AMC có
AM là cạnh chung
AB=AC (Do △ABC cân tại A0
BM=CM (vì M là chung điểm của BC)
a) Vẽ đúng hình:

Xét và có:
,
(do giả thiết cân tại
(do giả thiết là trung điểm của cạnh )
Do đó (c.g.c).
b) Do giả thiết , ;
, suy ra và là hai tam giác vuông (ở và ).
Mà , (chứng minh trong a)).
Do đó (cạnh huyền-góc nhọn).
Suy ra (cạnh tương ứng).
Mà nên .
c) cân ở (do theo chứng minh trên) nên
Tương tự, cân ở (giả thiết) nên
Do đó , suy ra // .
xét Δ AMB và Δ AMC có :
AM là cạnh chung
AB = AC
MB = MC
=> Δ AMB = Δ AMC ( C.C.C )
vì Δ ABC cân tại A
=> A1 = A2
xét Δ AME và Δ AMF có AEM = AFM = 90o A1 = A2 AM chung => Δ AME = Δ AMF ( CẠNH GÓC VUÔNG VÀ GÓC NHỌN KỀ) => EA = FA
a)
xét tam giác ABM và tam giác ACM có:
AB=AC(gt)
MB=MC(gt)
B=C(gt)
suy ra tam giác ABM=ACM(c.g.c)
b)
xét 2 tam giác vuông AHC và AKB có:
AB=AC(gt)
A(chung)
suy ra tam giác AHB=AKB(CH-GN)
suy ra AH=AK
AB=AC
BH=AB=AH
CK=AC-AK
từ tất cả nh điều trên suy ra BH=CK
c)
xét tam giác KBC và tma giác HCB có:
CB(chugn)
HB=KC(theo câu b)
B=C(gt)
suy ra tam giác KBC=ACB(c.g.c)
suy ra KBC=HCB suy ra tam giác IBC cân tại I
a) kẻ thêm từ A đến M
tam giác AMB = tam giác AMC vì
AM là cạnh chung
BM = CM ( tam giác cân )
góc M = 900
tam giác AMB = tam giác AMC (c.g.c)
b) gọi AEM và AFM là tam giác
tam giác AEM và tam giác AFM bằng nhau vì
góc AE = góc AF = 900 (GT)
AM là cạnh chung
⇒ EA = FA ( 2 cạnh góc vuông )
c) gọi 2 góc E và hai góc F là E1, E2, F1, F2
kẻ thêm từ E sang F
EF // BC vì
E1 + E2 + F1 + F2 = 1800 (góc bẹt)
B + E1 + F2 + C = 1800
⇒ EF // BC
a) Do đó tam giác AMB = tam giác AMC (c.g.c)
b) Mà AB = AC nên EA = AB - EB = AC - FC = FA.
c) Do đó góc AEF = góc ABC, suy ra EF // BC.
a) AB = AC (do ABC là tam giác cân)
Góc B = góc C
MB = MC ( M là trung điểm của cạnh BC)
Do đó ΔAMB = ΔAMC (c.g.c)
b) Vì góc MEB = góc MFC mà cạnh MB = MC mà góc B = góc C nên EM = MF (g.c.g)
Mà AB = AC nên EA = AB - EB = AC - FC = FA
c) Cho tâm của hình vuông AFME là O
Góc MOF = 90 độ suy ra hai góc còn lại mỗi góc bằng 45 độ
Góc MFC = 90 độ suy ra hai góc còn lại mỗi góc bằng 45 độ
Suy ra góc OFM = FMC ( hai góc so le trong)
Suy ra EF // BC
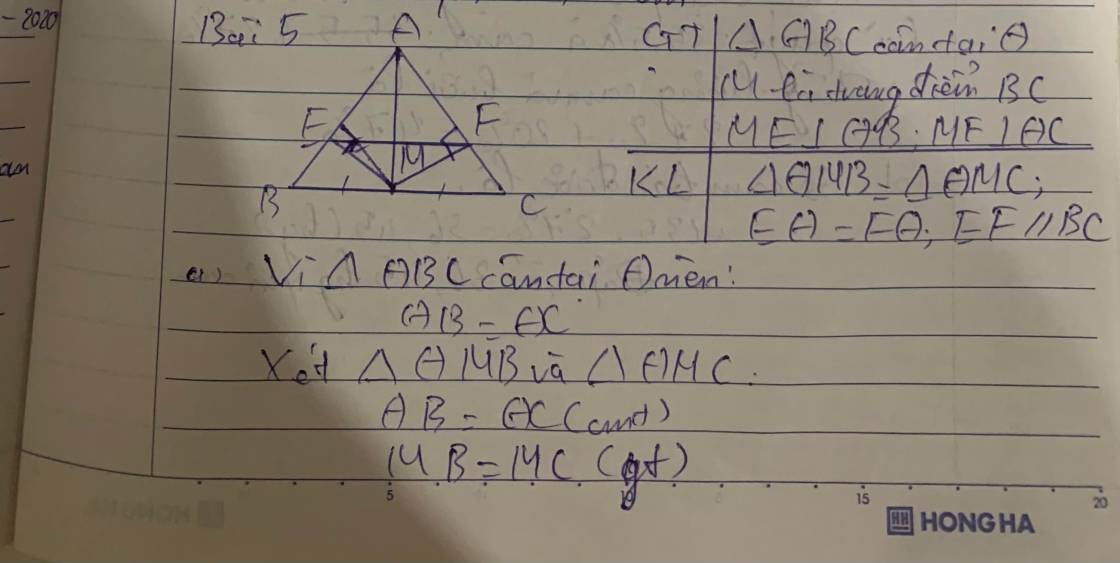
a) Xét tam giác ABC và tam giác AMC ta có :
Xét và có:
,
(m là trung đ BC)
Do đó (c.g.c).
b) Do giả thiết , ;
, suy ra và là hai tam giác vuông (ở và ).
Mà , (chứng minh trong a)).
Do đó (cạnh huyền-góc nhọn).
Suy ra (cạnh tương ứng).
Mà nên .
c) cân ở (do theo chứng minh trên) nên
Tương tự, cân ở (giả thiết) nên
Do đó , suy ra // .
xét △ABM và △ACM có
AB=AC (theo giả thiết)
= (theo giả thiết)
MB=MC (theo giả thiết)
⇒△ABM=△ACM (c.g.c)
⇒ = (hai góc tương ứng)
a) Xét \(\Delta AMC\) và \(\Delta AMB\) có
AB=AC
\(\widehat{B}=\widehat{C}\)
MB=MC
Do đó \(\Delta AMB=\Delta AMC\left(c.g.c\right)\)
b)Do giả thiết \(ME\perp AB\)
\(MF\perp AC\) suy ra và là hai tam giác vuông
Mà , \(\widehat{B}=\widehat{C}\)
Do đó (cạnh huyền-góc nhọn).
Suy ra (cạnh tương ứng).
Mà nên .
c)\(\Delta AEF\) cân ở (do theo chứng minh trên) nên \(\widehat{AEF}=\left(180^0-\widehat{A}\right):2\)
Tương tự, \(\Delta ABC\) cân ở (giả thiết) nên \(\widehat{ABC}=\left(180^0-\widehat{A}\right):2\)
Do đó \(\widehat{AEF}=\widehat{ABC}\), suy ra EF//BC
Xét và có:
,
(do giả thiết cân tại
(do giả thiết là trung điểm của cạnh )
Do đó (c.g.c).
b) Do giả thiết , ;
, suy ra và là hai tam giác vuông (ở và ).
Mà , (chứng minh trong a)).
Do đó (cạnh huyền-góc nhọn).
Suy ra (cạnh tương ứng).
Mà nên .
c) cân ở (do theo chứng minh trên) nên
Tương tự, cân ở (giả thiết) nên
Do đó , suy ra // .
a) Vẽ đúng hình:

Xét và có:
,
(do giả thiết cân tại
(do giả thiết là trung điểm của cạnh )
Do đó (c.g.c).
b) Do giả thiết , ;
, suy ra và là hai tam giác vuông (ở và ).
Mà , (chứng minh trong a)).
Do đó (cạnh huyền-góc nhọn).
Suy ra (cạnh tương ứng).
Mà nên .
c) cân ở (do theo chứng minh trên) nên
Tương tự, cân ở (giả thiết) nên
Do đó , suy ra // .
a, xét △ AMB và △ AMC có
AB=AC
B=C(do giả thiết △ ABC cân tại A)
MB=MC(do giả thiết M là trung điểm của cạnh BC)
vậy △ ABM=△ ACM
b, do giả thiết ME vuông góc với AB (E ϵ AB)
MF vuông góc với AC (F ϵ AC) suy ra △ EMB và △ FMC là tam giác vuông ở E và F)
mà MB = MC.B=C (chứng minh trong a)
do đó △EMB=△FMC (cạnh huyền-góc nhọn)
suy ra EB=FC (cạnh tương ứng)
mà AB=AC nên EA=AB-EB=AC-FC=FA
c, △AEF cân ở A (do EA = FA theo chứng minh trên) nên AEF = (180o- A):2
tương tự,△ABC cân ở A (giả thiết) nên ABC=(180o-A):2
do đó AEF = ABC, suy ra EF song song với BC
a)vì M là trung điểm của BC nên suy ra MB=MC và ΔABC là tam giác cân tại A nên 2 góc ở đáy bằng nhau suy ra góc ABM=góc ACM
xétΔAMB=ΔAMC ta có:
góc ABM=góc ACM=90\(^0\)
MB=MC(gt)
AM cạnh chung
suy ra tam giác .(2 cạnh góc vuông)
b)
478369IOQ34]PƠ\QEW
Ơpoiuytrewsedrtyuiopoi8u7y6t5r4e34r5t6y7u8i9o0oiuytrdefghjklbvcvbnm,kjhgfdtyui
a, Xét ΔAMB và ΔAMC có:
AB=AC(gt)
AM là cạnh chung
MB=MC(gt)
→ΔAMB=ΔAMC(c-c-c)
b,Xét ΔMEA và ΔMFA có:
ME=MF(gt)
MA là cạnh chung
EA=FA(gt)
→ΔMEA = ΔMFA(c-c-c)
c,Xét ΔMEF và ΔMBC có:
ME=MB(gt)
góc MEF=góc MBC(đối đỉnh)
EF=FA(gt)
→ΔMEF=ΔMBC(c-g-c)
→ góc E1= góc B1(2 góc tương ứng)
Mà 2 góc này nằm ở vị trí sole trong
→EF//BC.
ΔABC cân tại A, trung tuyến AM. Từ M kẻ ME⊥AB tại E, kẻ MF⊥AC tại F.
a) chứng minh: ΔBEM=ΔCFM
b) chứng minh AM là trung trực của EF.
c) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau tại D. Chứng minh rằng ba điểm A,M,D thẳng hàng