Question

Câu 10. Từ điểm A nằm ngoài đường tròn (0) kẻ các tiếp tuyến AB, AC đến đường tròn (B, C là tiếp điểm). Gọi H là giao điểm của OA và BC.
a. Chứng minh OB = OH.OA.
b. EF là một dây cung của (O) đi qua H sao cho A, E, F không thẳng hàng. Chứng minh bốn điểm A, E, O, F nằm trên cùng một đường tròn

Answer 1

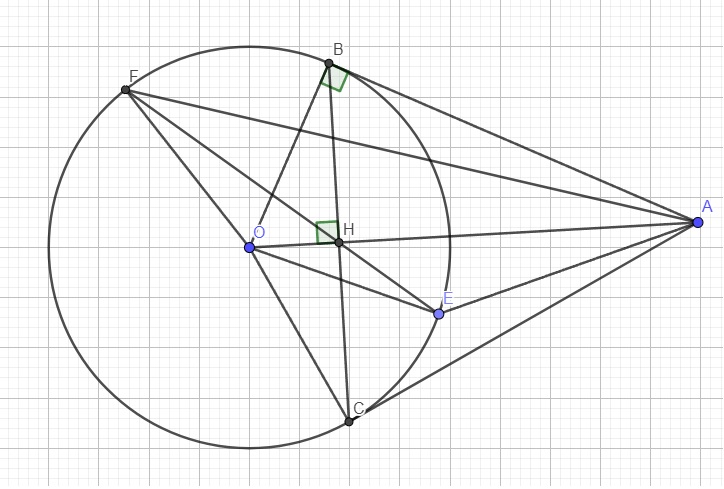
a. Chắc đề đúng là \(OB^2=OH.OA\)

Theo t/c hai tiếp tuyến cắt nhau: \(AB=AC\)

Lại có \(OB=OC=R\)

\(\Rightarrow OA\) là trung trực của BC

\(\Rightarrow OA\perp BC\) tại H đồng thời H là trung điểm BC

Cũng do AB là tiếp tuyến \(\Rightarrow AB\perp OB\Rightarrow\Delta OAB\) vuông tại B

Áp dụng hệ thức lượng trong tam giác vuông OAB:

\(OB^2=OH.OA\)

b.

Ta có: \(OF=OB=R\Rightarrow OF^2=OH.OA\)

\(\Rightarrow\dfrac{OF}{OH}=\dfrac{OA}{OF}\)

Xét hai tam giác OAF và OFH có:

\(\left\{{}\begin{matrix}\widehat{AOF}-chung\\\dfrac{OF}{OH}=\dfrac{OA}{OF}\end{matrix}\right.\) \(\Rightarrow\Delta OAF\sim\Delta OFH\left(c.g.c\right)\)

\(\Rightarrow\widehat{OAF}=\widehat{OFH}\) hay \(\widehat{OAF}=\widehat{OFE}\)

Mà \(OE=OF=R\Rightarrow\Delta OEF\) cân tại O \(\Rightarrow\widehat{OFE}=\widehat{OEF}\)

\(\Rightarrow\widehat{OAF}=\widehat{OEF}\)

Hai góc nói trên cùng chắn OF và cùng nằm trong nửa mặt phẳng bờ OF

\(\Rightarrow OEAF\) nội tiếp hay 4 điểm A, E, O, F cùng nằm trên 1 đường tròn

Answer 2