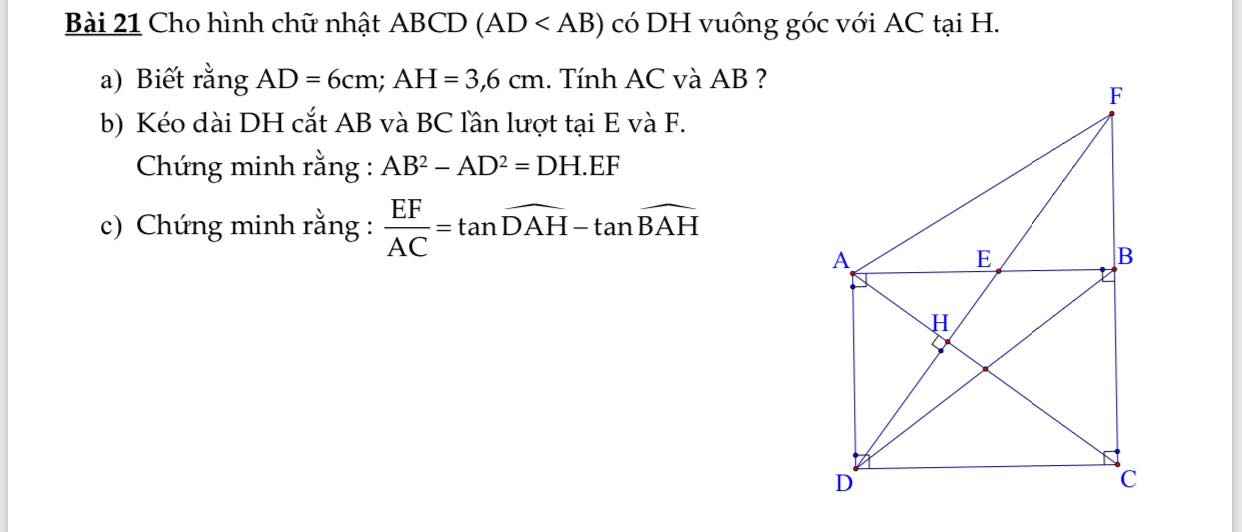
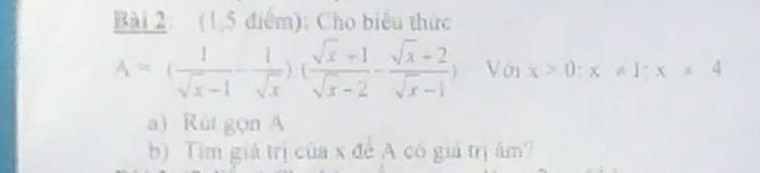Câu 1:
1: Thay x=9 vào B, ta được:
\(B=\dfrac{9-1}{2\cdot\sqrt{9}}=\dfrac{8}{2\cdot3}=\dfrac{4}{3}\)
2: P=AB
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{x+\sqrt{x}}{x-1}\right)\cdot\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x-1}{2\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}+1-x-\sqrt{x}}{2\sqrt{x}}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
3: \(\dfrac{1}{P}>=\dfrac{\sqrt{x}+9}{8}\)
=>\(\dfrac{2\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}+9}{8}>=0\)
=>\(\dfrac{16\sqrt{x}-\left(\sqrt{x}+1\right)\left(\sqrt{x}+9\right)}{8\left(\sqrt{x}+1\right)}>=0\)
=>\(16\sqrt{x}-\left(\sqrt{x}+1\right)\left(\sqrt{x}+9\right)>=0\)
=>\(16\sqrt{x}-x-10\sqrt{x}-9>=0\)
=>\(-x+6\sqrt{x}-9>=0\)
=>\(\left(\sqrt{x}-3\right)^2< =0\)
mà \(\left(\sqrt{x}-3\right)^2>=0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-3=0\)
=>x=9
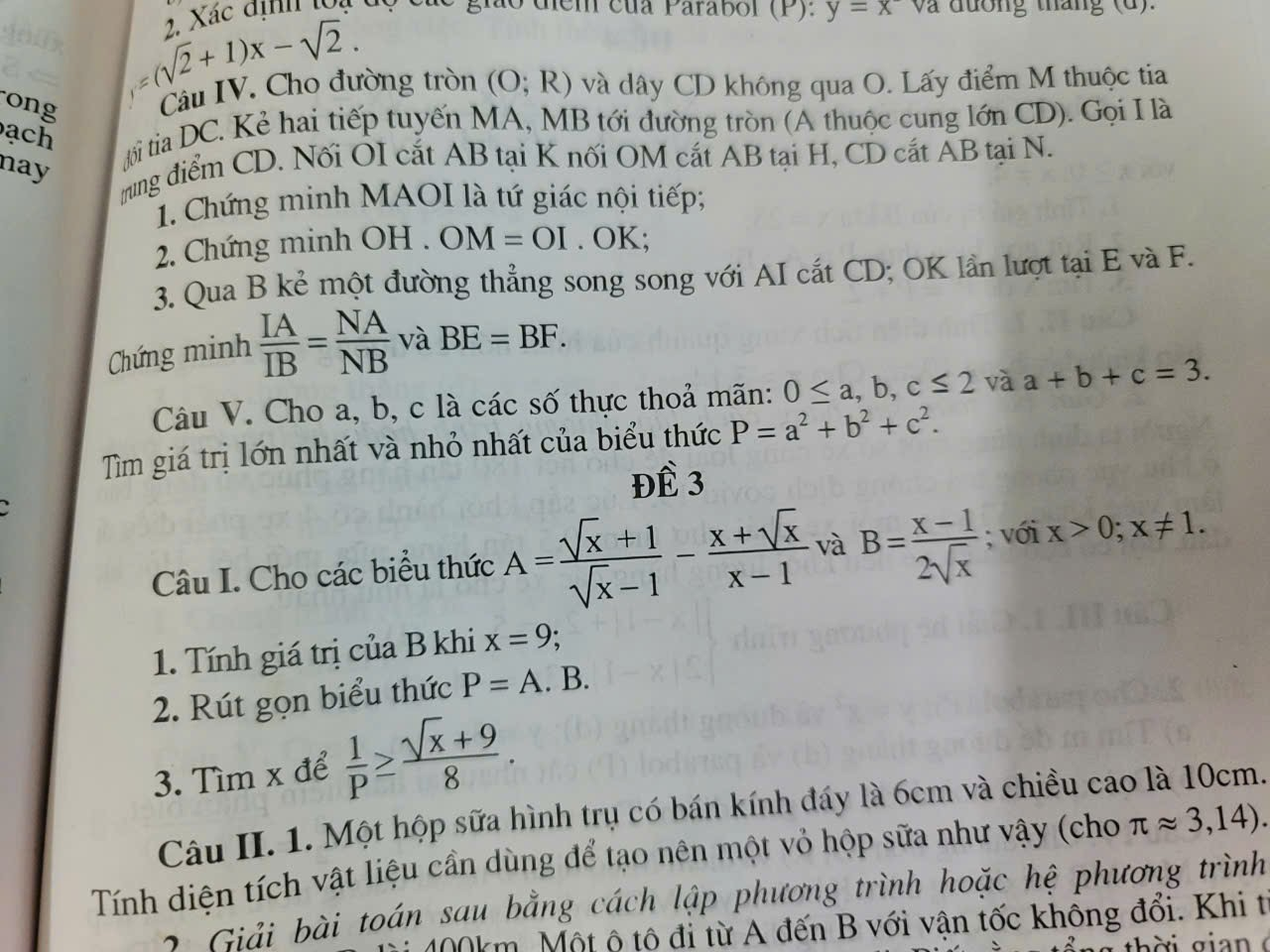
Giải giúp tớ với ạ, tớ cần gấp lắm
