Đáp án B.
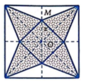
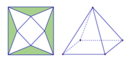
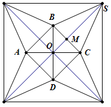
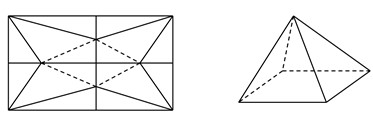
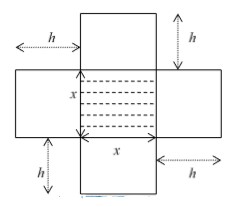
Sau khi cắt miếng giấy hình vuông như hình vẽ, ta xếp lại được thành hình chóp tứ giác đều S.MNPQ (hình bên).
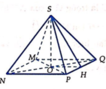 Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Gọi H là trung điểm P Q ⇒ O H = M N 2 = 2 x 2 (cm) và S H = 10 2 - 2 x 2 (cm).
Suy ra S O = S H 2 - O H 2 = 10 2 - 2 x 2 2 - 2 x 2 2 = 20 ( 10 - x ) .
Thể tích khối chóp S.MNPQ là:
V
M
N
P
Q
=
1
3
.
S
O
.
S
M
N
P
Q
=
1
3
20
(
10
-
x
)
.
2
x
2
=
20
3
(
40
-
4
x
)
.
x
4
→
V
M
N
P
Q
=
20
3
(
40
-
4
x
)
.
x
.
x
.
x
.
x
≤
20
3
40
-
4
x
+
x
+
x
+
x
+
x
5
=
256
10
3
Dấu “=” xảy ra ⇔ 40 - 4 x = x ⇔ x = 8 (cm).