Chọn C.
Phương pháp:
Sử dụng công thức tính thể tích khối trụ có chiều cao h và bán kính r là V = π τ 2 h .
Cách giải:

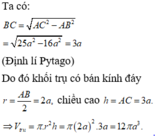
Chọn C.
Phương pháp:
Sử dụng công thức tính thể tích khối trụ có chiều cao h và bán kính r là V = π τ 2 h .
Cách giải:

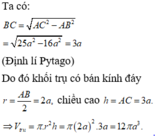
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, A B = 4 a , A C = 5 a . Thể tích của khối trụ là:
A. 16 π a 3
B. 12 π a 3
C. 4 π a 3
D. 8 π a 3
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD có AB và CD thuộc hái đáy của hình trụ, A B = 4 a , A C = 5 a Thể tích của khối trụ
A. 8 πa 3
B. 12 πa 3
C. 4 πa 3
D. 16 πa 3
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Cho hình trụ có bán kính đáy bằng a 2 . Cắt hình trụ bởi một mặt phẳng, song song với trụ của hình trụ và cách trục của hình trụ một khoảng bằng a 2 ta được thiết diện là một hình vuông. Tính thể tích V của khối trụ đã cho.
A. V = π a 3 3
B. V = π a 3 7 3
C. V = 2 π a 3 7
D. V = π a 3
khi cắt khối trụ (T) bởi mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a 3 ta được thiết diện là hình vuông có diện tích bằng 4 a 2 Tính thể tích V của khối trụ (T).
A. V = 7 7 π a 3
B. V = 7 7 π a 3 3
C. V = 8 3 π a 3
D. V = 8 π a 3
Khi cắt khối trụ (T) bởi một mặt phẳng song song với trục và cách trục của trụ (T) một khoảng bằng a 3 là được thiết diện là hình vuông có diện tích bằng 4 a 2 . Tính thể tích V của khối trụ (T)?.
A. V = 7 7 π a 3
B. V = 7 7 3 π a 3
C. V = 8 3 π a 3
D. V = 8 π a 3
Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính thể tích V của khối trụ tạo bởi hình trụ đó.
A. π 2
B. π
C. 2 π
D. 4 π
Cho hình trụ có bán kính đáy bằng a. Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng a 2 ta được thiết diện là một hình vuông. Tính thể tích khối trụ
A. π a 3 3 4
B. π a 3 3
C. π a 3
D. 3 π a 3
Cho khối trụ có chiều cao 20. Cắt khối trụ bởi một mặt phẳng ta được thiết diện là hình elip có độ dài trục lớn bằng 10. Thiết diện chia khối trụ ban đầu thành hai nửa, nửa trên có thể tích V 1 , nửa dưới có thể tích V 2 . Khoảng cách từ một điểm thuộc thiết diện gần đáy dưới nhất và điểm thuộc thiết diện xa đáy dưới nhất tới đáy lần lượt là 8 và 14. Tính tỉ số V 1 V 2
A. 9/11
B. 9/20
C. 6/11
D. 11/20