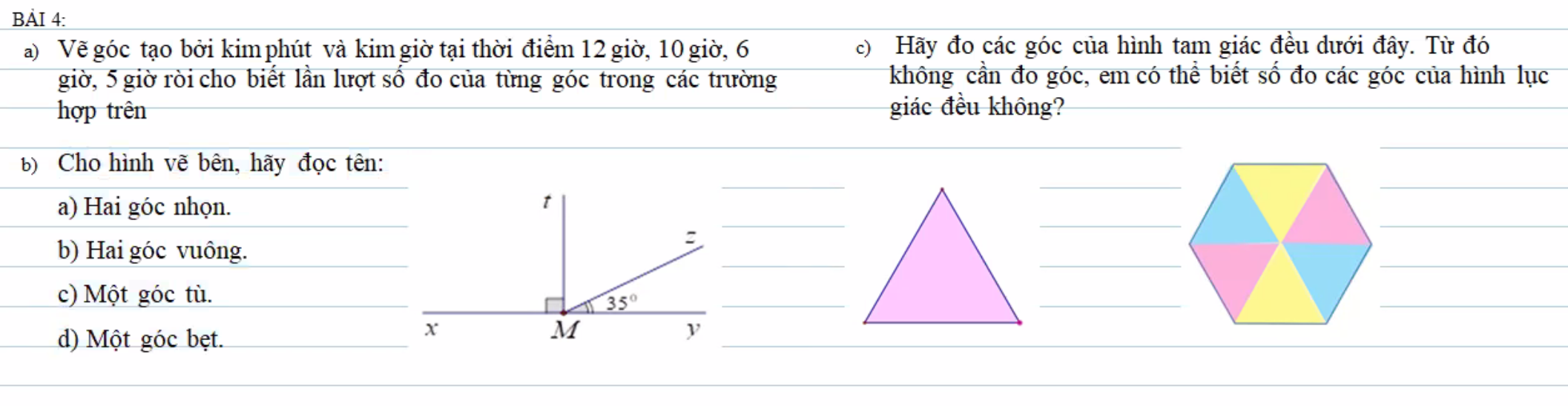
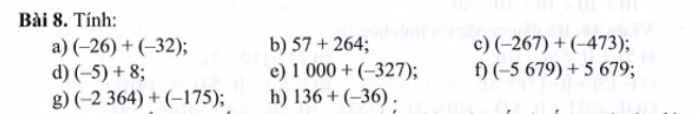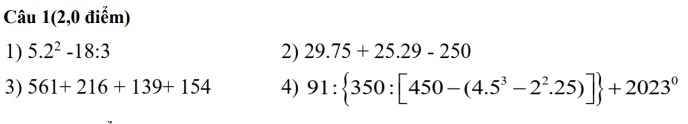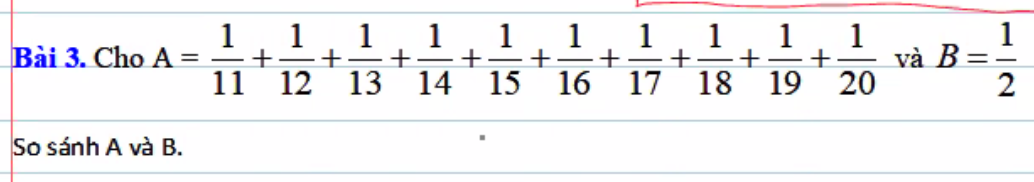e: \(17A=\dfrac{17^{2025}+17}{17^{2025}+1}=1+\dfrac{16}{17^{2025}+1}\)
\(17B=\dfrac{17^{2024}+17}{17^{2024}+1}=1+\dfrac{16}{17^{2024}+1}\)
\(17^{2025}+1>17^{2024}+1\)
=>\(\dfrac{16}{17^{2025}+1}< \dfrac{16}{17^{2024}+1}\)
=>\(\dfrac{16}{17^{2025}+1}+1< \dfrac{16}{17^{2024}+1}+1\)
=>17A<17B
=>A<B
g: \(10A=\dfrac{10^{2024}+50}{10^{2024}+5}=1+\dfrac{45}{10^{2024}+5}\)
\(10B=\dfrac{10^{2023}+50}{10^{2023}+5}=1+\dfrac{45}{10^{2023}+5}\)
ta có: \(10^{2024}+5>10^{2023}+5\)
=>\(\dfrac{45}{10^{2024}+5}< \dfrac{45}{10^{2023}+5}\)
=>\(\dfrac{45}{10^{2024}+5}+1< \dfrac{45}{10^{2023}+5}+1\)
=>10A<10B
=>A<B
h: \(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Ta có: \(2024^{2024}+1>2024^{2023}+1\)
=>\(\dfrac{2023}{2024^{2024}+1}< \dfrac{2023}{2024^{2023}+1}\)
=>\(1+\dfrac{2023}{2024^{2024}+1}< 1+\dfrac{2023}{2024^{2023}+1}\)
=>2024A<2024B
=>A<B