Bài `7`
\(\widehat {AOC} - \widehat {AOD} = 70^\circ\)
\(\widehat{AOC} + \widehat {AOD} = 180^\circ\) (hai góc kề bù)
\(=> \widehat{AOC} = (180 + 70) : 2 = 125^\circ\)
\(=>\widehat{AOD} = (180 - 70) : 2 = 55\)
Vì \(\widehat{AOC} ; \widehat {BOD}\) là `2` góc đối đỉnh và \(\widehat {AOC} = 125^\circ\) nên
\(=> \widehat {BOD} = 125^\circ\)
Vì \(\widehat {AOD} ; \widehat {COB}\) là `2` góc đối đỉnh và \(\widehat {AOD} = 55^\circ\) nên
\(=> \widehat {COB} = 55^\circ\)
`a,`
Vì \(\widehat{xOz} ; \widehat{zOy}\) là `2` góc kề bù nên
Ta có:
\(\widehat{xOz} + \widehat{zOy} = 180^\circ\)
\(60^\circ + \widehat{zOy} = 180^\circ\)
\(\widehat{zOy} = 180^\circ - 60^\circ\)
\(\widehat{zOy} = 120^\circ\)
`b,`
Vì \(\widehat {xOz} ; \widehat {nOy}\) là `2` góc đối đỉnh và \(\widehat{xOz} = 60^\circ\) nên
\(\widehat{nOy} = 60^\circ\)
Vì \(\widehat{nOx} ; \widehat{yOz}\) là `2` góc đối đỉnh và \(\widehat {yOz} = 120^\circ\) nên
\(\widehat{nOx} = 120^\circ\)
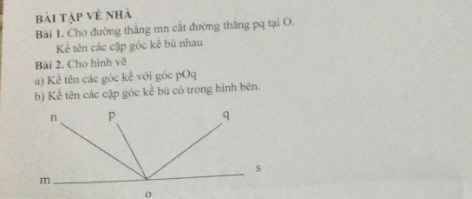
GIẢI GẤP GIÚP T Ạ, T CẦN GẤP 
