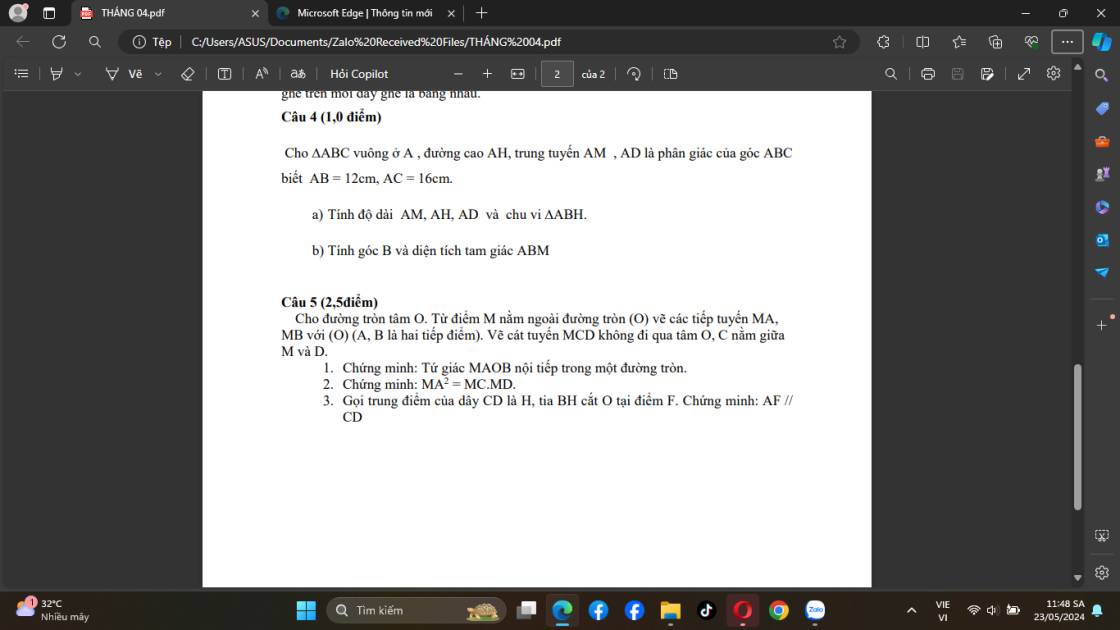
Câu 5:
1: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
2: Xét (O) có
\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{MAC}=\widehat{ADC}\)
Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó: ΔMAC~ΔMDA
=>\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\)
=>\(MA^2=MD\cdot MC\)
Câu 4:
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot20=12\cdot16=192\)
=>AH=192/20=9,6(cm)
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{BAC}{2}\right)\)
=>\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{24\cdot16}{28}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{48\sqrt{2}}{7}\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot20=12^2=144\)
=>BH=144/20=7,2(cm)
Chu vi tam giác ABH là:
AB+BH+AH
=7,2+12+9,6
=16,8+12=28,8(cm)
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{16}{20}=\dfrac{4}{5}\)
nên \(\widehat{B}\simeq53^0\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot12\cdot16=96\left(cm^2\right)\)
Vì MB=1/2BC nên \(S_{ABM}=\dfrac{1}{2}\cdot S_{ABC}=48\left(cm^2\right)\)
Câu 5c
Xét tứ giác OHAM có ^OHM = ^OAM = 900
Mà 2 góc này cùng nhìn cung OM
Vậy OHAM nội tiếp đường tròn
Lại có MAOB nội tiếp đường tròn (ý a)
=> B;M;A;H;O nội tiếp đường tròn
=> ^HBM = ^HMA = ^HOA( góc nt chắn cung HA) (1)
Cho DF giao MA tại I
Ta có ^FBA = ^FAI ( góc nt chắn cung FA, góc tạo bởi tiếp tuyến MA chắn cung FA) (2)
Từ (1) ; (2) => ^HMA = ^FAI
mà 2 góc này ở vị trí đồng vị => AF // CD
Câu 5
3: Xét (O) có:
A,F,D,C cùng thuộc đường tròn
=> AFDC là tứ giác nội tiếp
=> ∠AFD = ∠MCA (tự c/m)
Chỉ ra: AMOH và MBOH là tứ giác nội tiếp
=> M, A, H, O, B cùng thuộc 1 đường tròn
=> MAHB là tứ giác nội tiếp
=> ∠AMH = ∠ABH
Xét (O) có: ∠ABF = ∠ADF (2 góc nội tiếp cùng chắn cung AF)
Mà ∠AMH = ∠ABH => ∠AMH = ∠ADF
Xét ΔAMC có: ∠AMC + ∠MAC + ∠MCA = 180o
Mà ∠AMC = ∠ADF; ∠AMC = ∠MDA; ∠MCA = ∠AFD
=> ∠ADF + ∠MDA + ∠AFD = 180o
=> ∠FDM + AFD = 180o
Mà 2 góc ở vị trí trong cùng phía
=> AF // CD









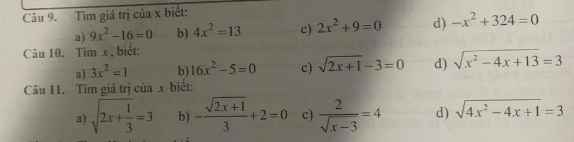












 giúp em với ạ, cần gấp ạ TvT
giúp em với ạ, cần gấp ạ TvT


 giải hộ mình vs ạ mình cần gấp ạ
giải hộ mình vs ạ mình cần gấp ạ

