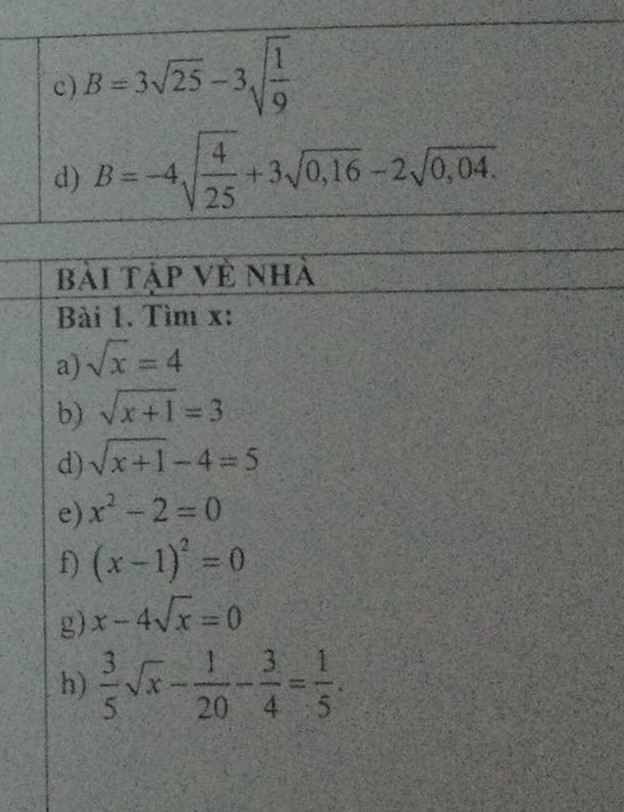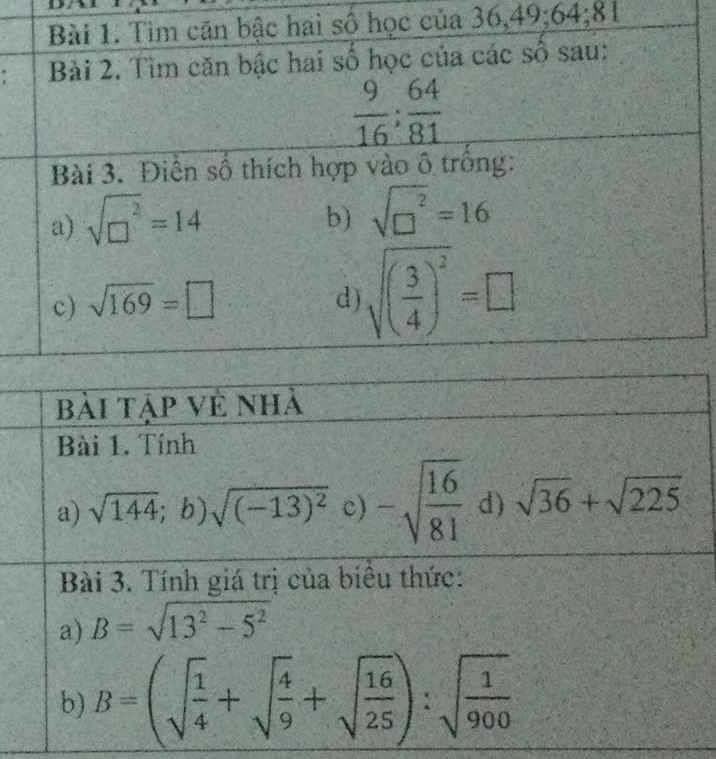a. Xét tg ABC cân tại A có: AB=AC; g ABC= gACB
Xét tgHAB và tgHCA có:
AH chung
gABH=gACH
AB=AC
=> tg HAB= tgHCA (cgc)
b. Xét tg BDH và tg CEH có:
BH = CH (H là trung điểm của BC)
g ECH = g EBH
=> tgBDH = tgCEH (ch-gn)
=> BD = CE (2 cạnh tương ứng)
Có: AB = AD + BD
AC = AE + CE
Mà BD = CE; AB = AC => AD = AE
=> tg ADE cân tại A
c. Xét tg BDH và tg KCH có:
HD = HK
BH = CH
gDHB=gCHK (đối đỉnh)
=> tg BDH = tgKCH (cgc)
=> BD = CK (2 cạnh tương ứng)
Trong tg DBH có: BD<BH (cạnh huyền và cạnh góc vuông)
Mà BD = CK => CK<HB













 giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ

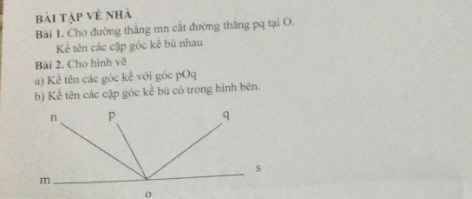
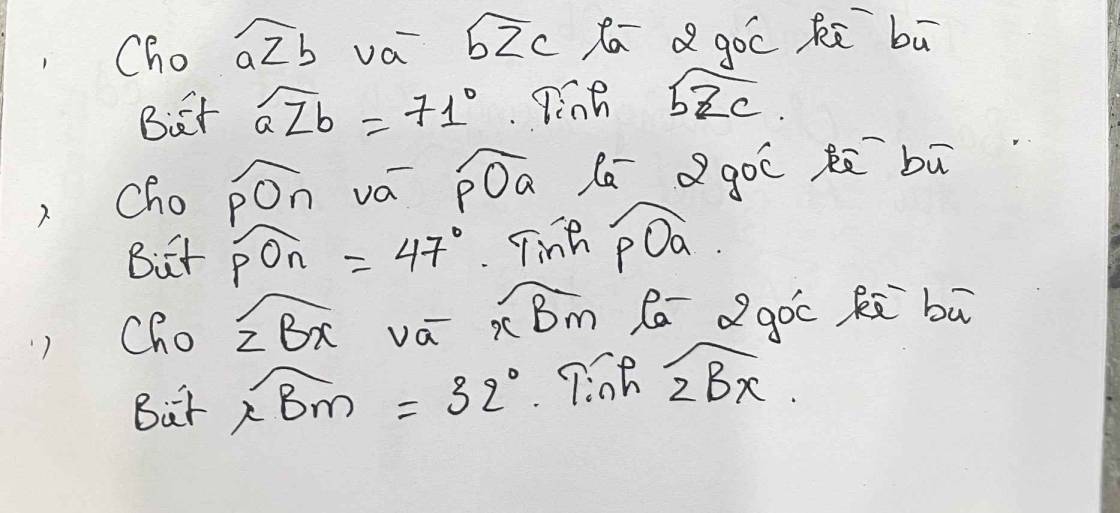 GIẢI GẤP GIÚP T Ạ, T CẦN GẤP
GIẢI GẤP GIÚP T Ạ, T CẦN GẤP