Question

cần câu d

Answer 1

    

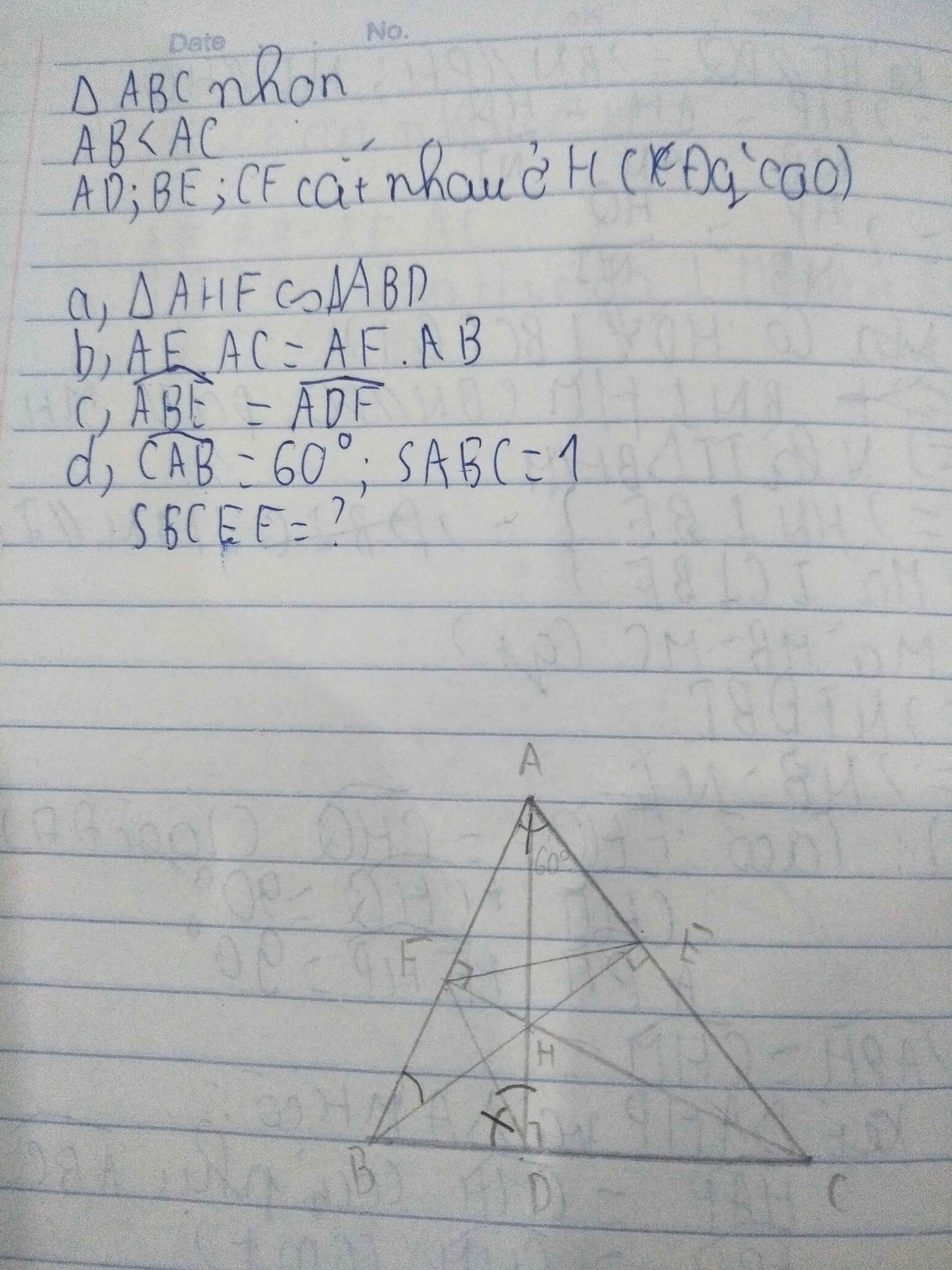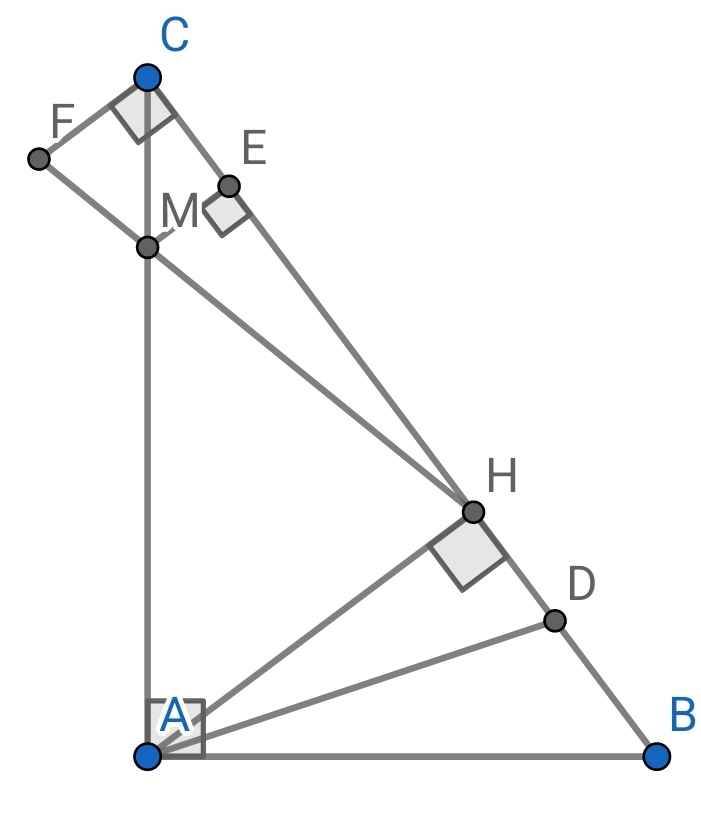
d) Do AH ⊥ BC (gt)

FC ⊥ BC (gt)

⇒ AH // FC

⇒ ∠AHM = ∠CFM (so le trong)

∠MAH = ∠FCM (so le trong)

∆AHM có:

∠AHM + ∠MAH + ∠AMH = 180⁰ (tổng ba góc trong ∆AHM)

⇒ ∠AMH = 180⁰ - (∠AHM + ∠MAH)

∆CFM có:

∠CFM + ∠FCM + ∠CMF = 180⁰ (tổng ba góc trong ∆CFM)

⇒ ∠CMF = 180⁰ - (∠CFM + ∠FCM)

Mà ∠CFM = ∠AHM (cmt)

∠FCM = ∠MAH (cmt)

⇒ ∠AMH = ∠CMF

Lại có:

∠CMH + ∠AMH = 180⁰ (kề bù)

⇒ ∠CMH + ∠CMF = 180⁰

⇒ H, M, F thẳng hàng