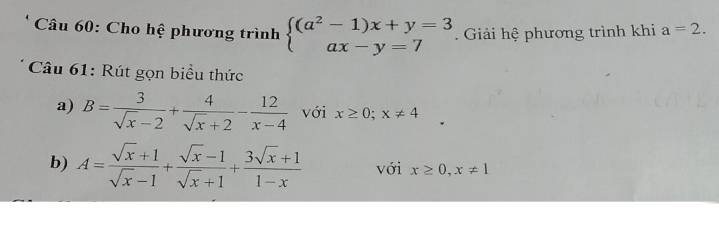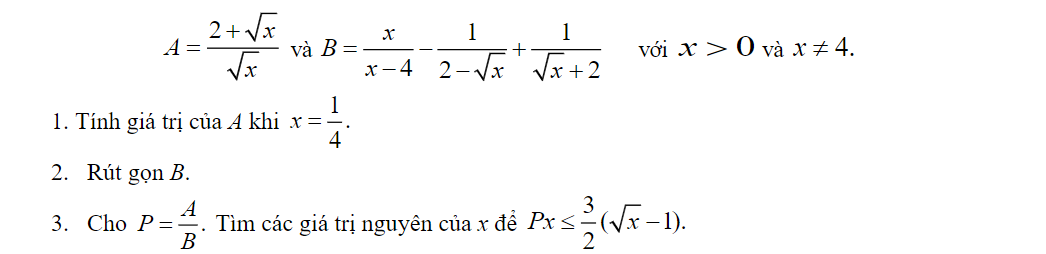Bài toán này bị biến đổi:
Em chỉ cần chuyển 1 chút xíu là thấy dạng chuẩn của nó:
\(P=\dfrac{a^3+1}{b^3+1}+\dfrac{b^3+1}{c^3+1}+\dfrac{c^3+1}{a^3+1}-3\)
Đặt \(\left(a^3+1;b^3+1;c^3+1\right)=\left(x;y;z\right)\Rightarrow x;y;z\in\left[1;2\right]\)
Quy về bài toán: cho các số \(x;y;z\in\left[1;2\right]\) (đồng thời \(x+y+z\le4\), cái này thậm chí ko cần), chứng minh \(\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\le\dfrac{7}{2}\)
Điều kiện ban đầu \(a+b+c=1\) mặc dù ko cần tận dụng hết, nhưng may mắn là dấu "=" vẫn xảy ra thỏa mãn \(a+b+c=1\)
Do BĐT là hoán vị theo x;y;z, ko mất tính tổng quát, giả sử \(y=mid\left\{x;y;z\right\}\)
\(\Rightarrow\left(x-y\right)\left(y-z\right)\ge0\)
\(\Leftrightarrow xy+yz\ge y^2+xz\)
\(\Leftrightarrow\dfrac{x}{z}+1\ge\dfrac{x}{y}+\dfrac{y}{z}\)
\(\Rightarrow\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\le\dfrac{x}{z}+\dfrac{z}{x}+1\)
- Nếu \(2\ge x\ge y\ge z\ge1\Rightarrow1\le\dfrac{x}{z}\le2\)
Đặt \(\dfrac{x}{z}=t\in\left[1;2\right]\Rightarrow\) cần c/m \(t+\dfrac{1}{t}+1\le\dfrac{7}{2}\)
\(\Leftrightarrow\dfrac{\left(2t-1\right)\left(t-2\right)}{2t}\le0\) (đúng)
- Nếu \(2\ge z\ge y\ge x\ge1\) dặt \(t=\dfrac{z}{x}\in\left[1;2\right]\)
Y hệt trường hợp bên trên
Vậy \(P\le\dfrac{7}{2}-3=\dfrac{1}{2}\)
Dấu "=" xảy ra tại \(\left(0;0;1\right)\) và vài hoán vị
anh ơi, câu này dùng hàm bậc nhất ạ, e có lm rồi nhưng sợ sai ý