Do 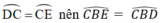 ( hai góc nội tiếp chắn hai cung bằng nhau).
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc 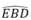 .
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.
Do 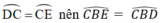 ( hai góc nội tiếp chắn hai cung bằng nhau).
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc 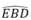 .
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90 ° ) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng:
a) CD = CE ; b) ΔBHD cân ; c) CD = CH.
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng: CD = CH
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng: CD = CE
Câu 3: Cho tam giác ABC (góc C khác 90 độ ), nội tiếp đường tròn tâm O các đường cao hạ từ A và B cắt nhau lại H và các cạnh BC và AC lần lượt tại I và K cắt đường tròn tại D và E .CMR a)Chứng minh tứ giác CIHK nội tiếp b) Chứng minh CE = CD C) Chứng minh tam giác BDH cân.
Cho đường tròn (O). Các đường cao BE và CF của tam giác ABC cắt nhau tại H và cắt (O) lần lượt tại E' và F' (E' khác B và F' khác C).
a, Chứng minh tứ giác BCEF nội tiếp
b, Chứng minh EF//E'F'
c, Kẻ OI vuông góc với BC( I thuộc BC). Đường thẳng vuông góc với HI tại H cắt đường thẳng AB tại M và cắt đường thẳng AC tại N. Chứng minh tam giác IMN cân
Cho tam giác ngọn ABC hai đường cao hạ từ A và B cắt nhau tại H và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E chứng minh
a. CD=CE
b. CH vuông góc AB
c. Gọi I là giao điểm của AB và BC, K là giao điểm củaBE và AC. Chứng minh tứ giác AKIB nội tiếp xác định tâm đường tròn ngoại tiếp tứ giác AKIB
Giải giúp tớ với ạ mai mình phải nộp r help
Cho tam giác ABC nhọn nội tiếp đường tròn o các đường phân giác của góc b góc c cắt nhau tại I và cắt đường tròn lần lượt tại d f da dce cắt dây AC tại h và k a chứng minh tam giác ahk cân b các các từ giác nối tiếp các ICC hiden nối tiếp c tự giác akih là hình gì vì sao d tứ giác ABCD và có thêm điều kiện gì để tự giác ADIE là hình thoi
Các đường cao AM, BN của tam giác ABC cắt nhau tại H. Các đường cao ấy kéo dài cắt đường tròn ngoại tiếp tam giác ABC tại D và E.
Chứng minh rằng
a) ABMNlaf tứ giác nội tiếp
b) CD = CE
c) Các đường tròn ngoại tiếp các tam giác ABC và AHC có bán kính bằng nhau
Cho các đường cao tại A và B của tam giác ABC cắt nhau tại H(góc C khác 90°)và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E
1.Kẻ đường kính AG.Chứng minh BHCG là hình bình hành
2.Gọi I là giao của HG và BC. Chứng minh AH=2OI(O là tâm đường tròn ngoại tiếp tam giác ABC)
3.Gọi K là giao của AD và BC,M là giao của BE và AC. Chứng minh rằng KM//ED
4'.Cho BC cố định,A di động trên cung BC lớn. Chứng minh H thuộc 1 đường cố định
5.Cho góc BÁC bằng 60°. Chứng minh rằng AH=Ao