a) * Cách 1.

b) Do 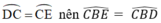 ( hai góc nội tiếp chắn hai cung bằng nhau).
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc 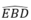 .
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.


a) * Cách 1.

b) Do 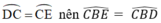 ( hai góc nội tiếp chắn hai cung bằng nhau).
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc 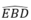 .
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.

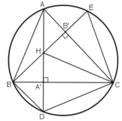
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng: ΔBHD cân
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng: CD = CE
Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90o) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng: CD = CH
Câu 3: Cho tam giác ABC (góc C khác 90 độ ), nội tiếp đường tròn tâm O các đường cao hạ từ A và B cắt nhau lại H và các cạnh BC và AC lần lượt tại I và K cắt đường tròn tại D và E .CMR a)Chứng minh tứ giác CIHK nội tiếp b) Chứng minh CE = CD C) Chứng minh tam giác BDH cân.
Cho tam giác ngọn ABC hai đường cao hạ từ A và B cắt nhau tại H và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E chứng minh
a. CD=CE
b. CH vuông góc AB
c. Gọi I là giao điểm của AB và BC, K là giao điểm củaBE và AC. Chứng minh tứ giác AKIB nội tiếp xác định tâm đường tròn ngoại tiếp tứ giác AKIB
Giải giúp tớ với ạ mai mình phải nộp r help
Các đường cao AM, BN của tam giác ABC cắt nhau tại H. Các đường cao ấy kéo dài cắt đường tròn ngoại tiếp tam giác ABC tại D và E.
Chứng minh rằng
a) ABMNlaf tứ giác nội tiếp
b) CD = CE
c) Các đường tròn ngoại tiếp các tam giác ABC và AHC có bán kính bằng nhau
Hai đường cao AK và BI của tam giác ABC giao nhau tại H (góc C khác 90o) và giao đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. C/m:
a. ABIK là tứ giác nội tiếp
b. CD=CE
c. Tam giác BHD cân
d. IK//ED
Cho tam giác ABC vuông tại A, có đường cao AH ( AB < AC ). Vẽ đường tròn (B;
BA) cắt đường thẳng AH tại D) (D khác A).
a) Chứng minh H là trung điểm của AD và tam giác CAD cân.
b) Chứng minh CD là tiếp tuyến của đường tròn (B; BA).
c) Vẽ đường kính AK của đường tròn (B;BA). Từ K vẽ đường thẳng vuông góc với AK cắt
đường thẳng AD tại N. Chứng minh DN.DC = DB.DK
d) Từ điểm M thuộc cung nhỏ AD của đường tròn (B;BA) vẽ tiếp tuyến cắt AC và CD lần
lượt tại E và F. Chứng minh rằng: Nếu diện tích tứ giác ABDC gấp 4 lần diện tích tam giác EBF
thì CE +CF = 3EF .
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Tiếp tuyến tại \(A\) với đường tròn ngoại tiếp tam giác \(ABC\) cắt các tiếp tuyến tại \(B\) và \(C\) lần lượt của \(D\) và \(E\). Gọi \(I\) là giao điểm \(CD\) và \(BE\). Chứng minh rằng:
\(a\)) \(A,I,H\) thẳng hàng.
\(b\)) \(AI=IH\).
\(c\)) \(DE\cdot AI=DB\cdot EC\)