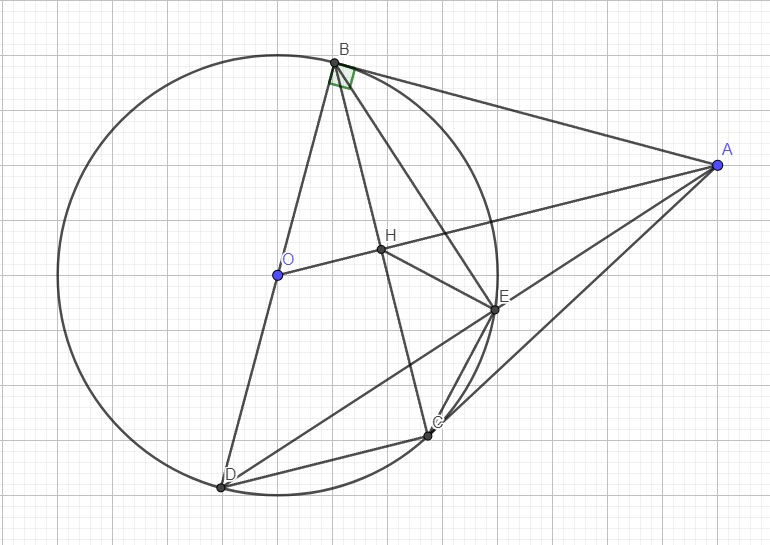
Các bạn vẽ hộ mình nữa nhé mik cảm ơn nhìu. Bài 1 : Cho đường tròn (O;R) và điểm A nằm ngoài (O). Từ A kẻ tiếp tuyến AB, AC với (O) (biết B,C là các tiếp điểm). Gọi H là giao điểm của OA và BC. a) Cm 4 điểm A,B,O,C cùng thuộc 1 đường tròn (Cm theo 2 △ nội tiếp, cm theo kiểu vì nó tiếp tuyến nên suy ra 2 cái đó vuông suy ra 4 điểm đó cùng thuộc 1 đg tròn). b) Lấy D là điểm đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) ( E ko trùng với D). Cm \(\dfrac{DE}{BE}=\dfrac{BD}{BA}\) và tính số đo của góc \(\widehat{HEC}\)
a.
Do AB là tiếp tuyến \(\Rightarrow AB\perp OB\Rightarrow\Delta ABO\) vuông tại B
\(\Rightarrow\) 3 điểm A, B, O cùng thuộc đường tròn đường kính OA
Tương tự, do AC là tiếp tuyến \(\Rightarrow\) 3 điểm A, C, O cùng thuộc đường tròn đường kính OA
\(\Rightarrow\) 4 điểm A, B, C, O cùng thuộc đường tròn đường kính OA
b.
Do D đối xứng B qua O \(\Rightarrow BD\) là 1 đường kính của (O)
\(\Rightarrow\widehat{BED}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{BED}=90^0\)
Xét hai tam giác vuông ABD và BED có:
\(\left\{{}\begin{matrix}\widehat{ABD}=\widehat{BED}=90^0\\\widehat{ADB}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta ABD\sim\Delta BED\left(g.g\right)\)
\(\Rightarrow\dfrac{DE}{BD}=\dfrac{BE}{BA}\Rightarrow\dfrac{DE}{BE}=\dfrac{BD}{BA}\)
Ta có: \(\left\{{}\begin{matrix}AB=AC\\OB=OC\end{matrix}\right.\) \(\Rightarrow OA\) là trung trực BC \(\Rightarrow OA\perp BC\) tại H
\(\Rightarrow H\) và E cùng nhìn AB dưới 1 góc vuông \(\Rightarrow ABHE\) nội tiếp
\(\Rightarrow\widehat{BEH}=\widehat{BAH}\) (cùng chắn AH)
Mà \(\widehat{BAH}=\widehat{CBD}\) (cùng phụ \(\widehat{AOB}\))
\(\widehat{CBD}=\widehat{CED}\) (cùng chắn CD)
\(\Rightarrow\widehat{BEH}=\widehat{CED}\)
Mà \(\widehat{BEH}+\widehat{HED}=\widehat{BED}=90^0\)
\(\Rightarrow\widehat{CED}+\widehat{HED}=90^0\)
\(\Rightarrow\widehat{HEC}=90^0\)