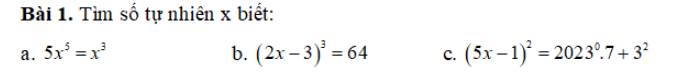a: \(5x^5=x^3\)
=>\(5x^5-x^3=0\)
=>\(x^3\left(5x^2-1\right)=0\)
=>\(\left[{}\begin{matrix}x^3=0\\5x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=\dfrac{1}{\sqrt{5}}\left(loại\right)\\x=-\dfrac{1}{\sqrt{5}}\left(loại\right)\end{matrix}\right.\)
b: \(\left(2x-3\right)^3=64\)
=>2x-3=4
=>2x=7
=>\(x=\dfrac{7}{2}\left(loại\right)\)
c: \(\left(5x-1\right)^2=2023^0\cdot7+3^2\)
=>\(\left(5x-1\right)^2=7+9=16\)
=>\(\left[{}\begin{matrix}5x-1=4\\5x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)
a. 5x = x³ Để giải phương trình này, ta chuyển vế và sử dụng tính chất nhân đôi: 5x - x³ = 0 x(5 - x²) = 0 x = 0 hoặc x = √5 hoặc x = -√5 Vậy phương trình này có ba nghiệm là 0, √5 và -√5. b. (2x-3)² = 64 Để giải phương trình này, ta bật căn và dùng quy tắc khai căn bậc hai của cả hai vế: 2x - 3 = ±8 2x = 3 ± 8 x = (-5/2) hoặc x = 11/2 Vậy phương trình này có hai nghiệm là (-5/2) và (11/2). c. (5x-1) = 2023°.7 + 32 Để giải phương trình này, ta giải bên trái để tìm giá trị của x: 5x - 1 = 2023°.7 + 32 5x = 2023°.7 + 33 x = (2023°.7+33)/5 Đây chính là giá trị của x để phương trình trở thành đúng. Ta có thể tính giá trị này bằng cách dùng máy tính hoặc phương pháp tính xấp xỉ