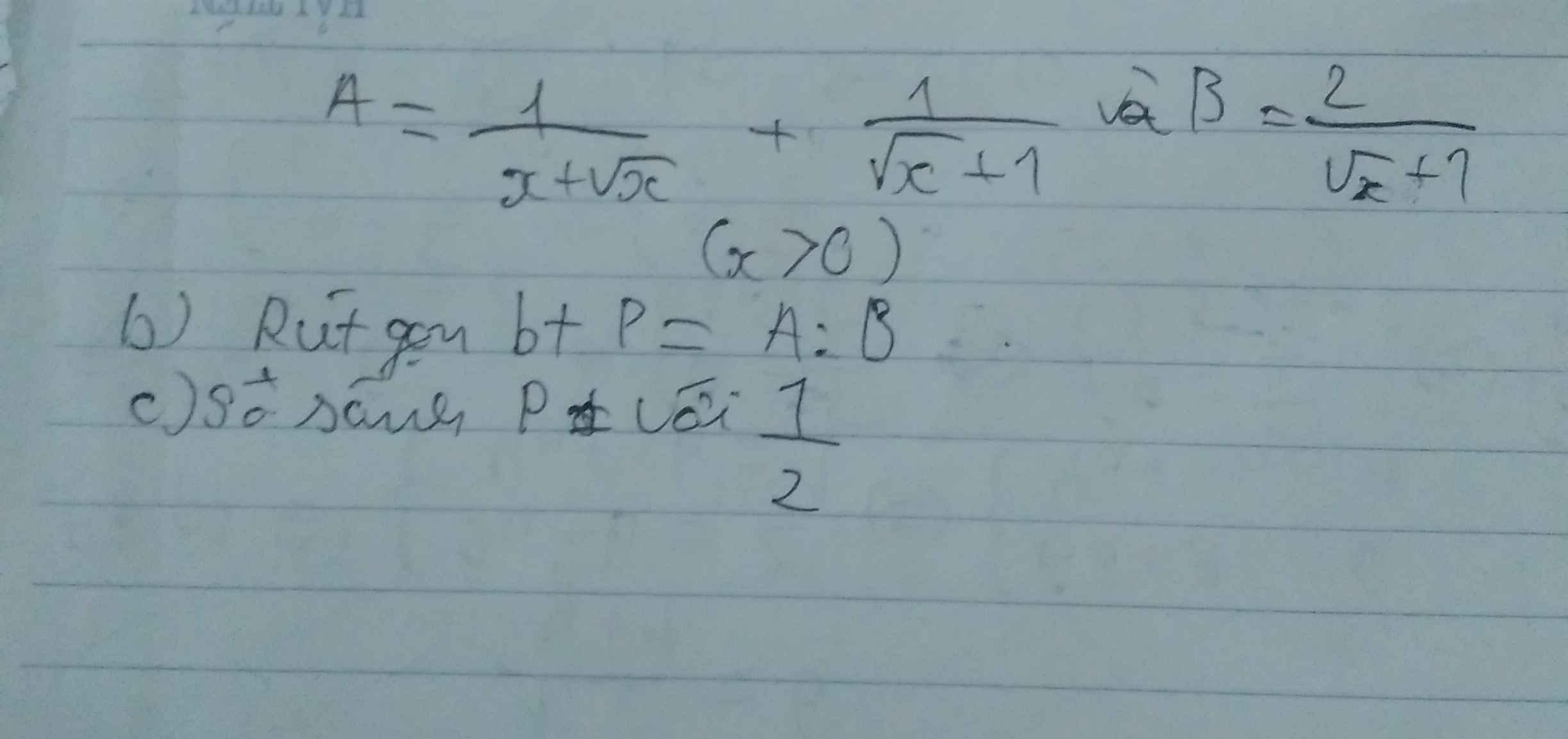Question

Các bạn ơi giúp mình với

Answer 1

a, Ta có : \(A=\dfrac{1}{x+\sqrt{x}}+\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}+1}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(1+\sqrt{x}\right)}=\dfrac{1}{\sqrt{x}}\)

\(\Rightarrow P=\dfrac{A}{B}=\dfrac{\dfrac{1}{\sqrt{x}}}{\dfrac{2}{\sqrt{x}+1}}=\dfrac{1}{\sqrt{x}}.\dfrac{\sqrt{x}+1}{2}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)

b, Ta có : \(P=\dfrac{\sqrt{x}+1}{2\sqrt{x}}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{x}}\)

Mà \(x>0\)

\(\Rightarrow\dfrac{1}{2\sqrt{x}}>0\)

\(\Rightarrow P>\dfrac{1}{2}\)

Vậy ...