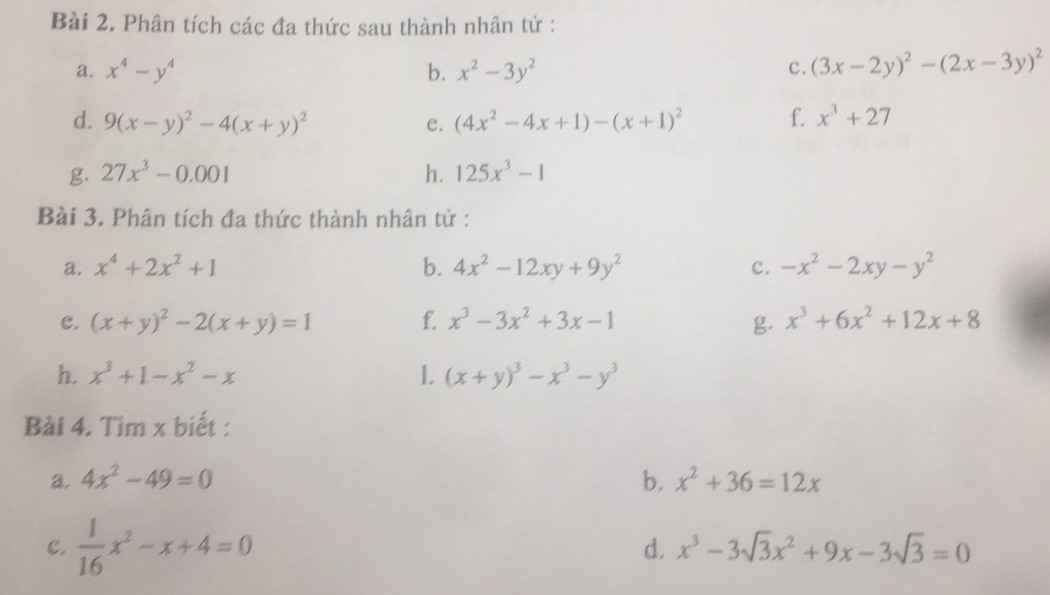`(x^4-1)^2+(x^2+1)^2`
`=x^8-2x^4+1+x^4+2x^2+1`
`=x^8-x^4+2x^2+2`
\(\left(x^4-1\right)^2+\left(x^2+1\right)^2=\left(x^2-1\right)^2.\left(x^2+1\right)^2+\left(x^2+1\right)^2\)
\(=\left(x^2+1\right)^2\left[\left(x^2-1\right)^2+1\right]=\left(x^2+1\right)^2\left(x^4-2x^2+2\right)\)
`(x^4-1)^2+(x^2+1)^2`
`=[(x^2)^2-1^2]^2+(x^2+1)^2`
`=(x^2+1)^2 .(x^2-1)^2 +(x^2+1)^2`
`=(x^2+1)^2 [(x^2-1)^2+1]`