Ta có :
\(x+y+z=0\)
\(\Rightarrow\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2\left(xy+yz+zx\right)=0\)
\(\Rightarrow xy+yz+zx=\dfrac{-\left(x^2+y^2+z^2\right)}{2}=-1012\) vì \(x^2+y^2+z^2=2024\)
\(\Rightarrow\left(xy+yz+zx\right)^2=x^2y^2+y^2z^2+z^2x^2+2xyz\left(x+y+z\right)=1012^2\)
\(\Rightarrow x^2y^2+y^2z^2+z^2x^2=1012^2\left(1\right)\) vì \(x+y+z=0\)
Ta lại có :
\(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(\Rightarrow B=x^4+y^4+z^4=\left(x^2+y^2+z^2\right)^2-2\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(\Rightarrow B=x^4+y^4+z^4=2024^2-2.1012^2\) vì \(\left(1\right)\)
\(\Rightarrow B=x^4+y^4+z^4=1012^2\left(2^2-2\right)=2.1012^2\)

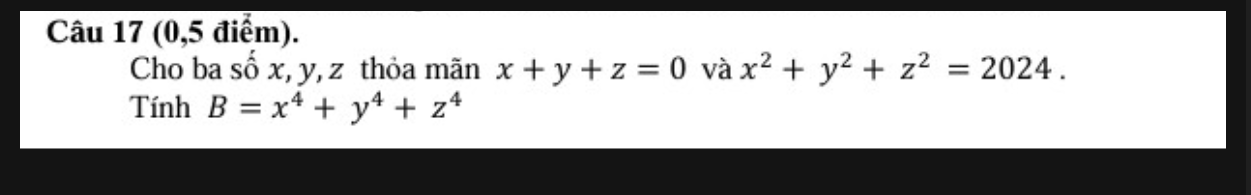 các bạn giúp mình với, mình cần gấp, cảm ơn nhìu nha(o゜▽゜)o❤
các bạn giúp mình với, mình cần gấp, cảm ơn nhìu nha(o゜▽゜)o❤











