\(1,M=\left(\dfrac{\dfrac{2}{5}-\dfrac{2}{9}+\dfrac{2}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{6}-\dfrac{7}{8}+\dfrac{7}{10}}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}-\dfrac{\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}}{\dfrac{7}{2}\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}\right)}\right)\cdot\dfrac{2013}{2012}\\ M=\left(\dfrac{2}{7}-\dfrac{2}{7}\right)\cdot\dfrac{2013}{2012}=0\)
\(\left|x^2+\left|x-2\right|\right|=x^2+2021\\ \Leftrightarrow\left[{}\begin{matrix}x^2+\left|x-2\right|=x^2+2021\\x^2+\left|x-2\right|=-x^2-2021\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left|x-2\right|=2021\\\left|x-2\right|=-2x^2-2021\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x-2=\pm2021\\x\in\varnothing\left(-2x^2-2021< 0\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2023\\x=-2019\end{matrix}\right.\)
\(3,\\ A=\left(x-\dfrac{2}{5}\right)^2+\left(y+20\right)^{10}+2022\ge2022\\ A_{min}=2022\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{2}{5}=0\\y+20=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-20\end{matrix}\right.\)
Các bạn giúp mình làm bài này gấp nhé!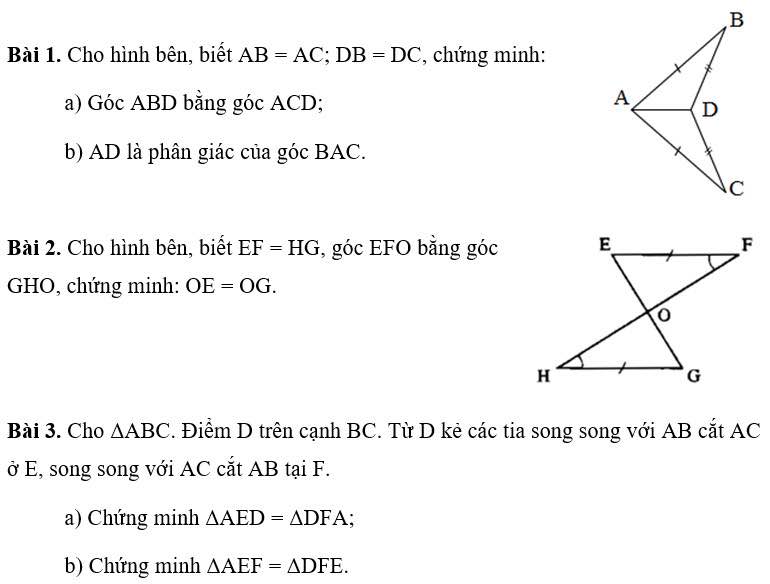
Các bạn làm giúp mình mấy bài này gấp nhé chiều nay mình phải nộp rồi
